Edited by Valentin Fadeev, Sunday 14 March 2010 at 14:43
Another surprising appearance of a fine method in a clumsy problem is offered when calculating optimal parameters for a pile of unitary cargo (bales, cases, crates etc).
Say we have bales of cotton stowed in several layers. According to safety regulations the pile must have a pyramid-like structure with "stairs" after certain amount of layers. Suppose we have 1 layer in the upper tier x bales long and y bales wide:
The next tier has 3 layers and is 2 bales longer (x+2) and 1 bale wider (y+1). What should be the values of x and y so that area occupied by the pile is minimized? Assume we have a fixed and sufficiently large total amount of bales, say 60.
If we behave negligently enough to give x and y continuous values (which is not so bad when total cargo count is high), the problem yields a nice solution using.. Lagrange multipliers:
Really, if one can use a scalpel as a screwdriver, that's what I am doing, but like in the previous case, it just looks nice
Calculus of Warehouses. Part 2
Another surprising appearance of a fine method in a clumsy problem is offered when calculating optimal parameters for a pile of unitary cargo (bales, cases, crates etc).
Say we have bales of cotton stowed in several layers. According to safety regulations the pile must have a pyramid-like structure with "stairs" after certain amount of layers. Suppose we have 1 layer in the upper tier x bales long and y bales wide: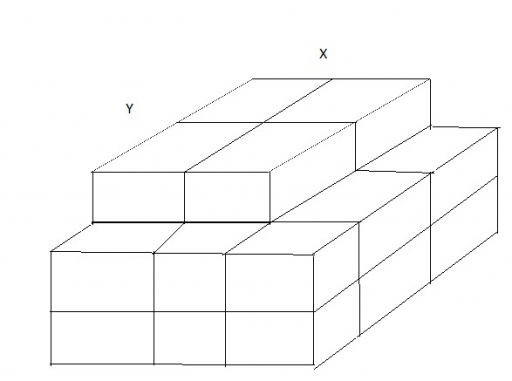
The next tier has 3 layers and is 2 bales longer (x+2) and 1 bale wider (y+1). What should be the values of x and y so that area occupied by the pile is minimized? Assume we have a fixed and sufficiently large total amount of bales, say 60.
If we behave negligently enough to give x and y continuous values (which is not so bad when total cargo count is high), the problem yields a nice solution using.. Lagrange multipliers:
Really, if one can use a scalpel as a screwdriver, that's what I am doing, but like in the previous case, it just looks nice