OU blog

Personal Blogs

Valentin Fadeev

Back to school

Saturday, 15 Jan 2011, 18:52
Visible to anyone in the world
Edited by Valentin Fadeev, Sunday, 18 Sep 2011, 23:24

This is problem 1.18 from JS (M821 course book). The question is to investigate the motion of a bead that slides on a smooth parabolic wire rotating with constant angular velocity omega about a vertical axis. x is the distance from the axis of rotation.

To simplyfy the calculations we can choose the scale so that equation of the parabola is y equals x squared divided by two .

Yes, I know as a grown up man I should write out the expression of the kinetic energy:

equation sequence cap t equals m times v squared divided by two plus m times omega squared times x squared divided by two equals m divided by two times open d times s divided by d times t close squared plus m times omega squared times x squared divided by two

where v is the tangential velocity of the bead directed along the wire. Then define potential energy as usual:

equation sequence cap v equals negative integral f of y d y equals integral m times g d y equals m times g times y equals m times g times x squared divided by two

bearing in mind that the force of gravity acts in the direction opposite to that of cap y axis, hence changing the sign.

Construct the Lagrangian:

equation sequence script cap l equals cap t minus cap v equals m divided by two times open d times s divided by d times t close squared plus m times omega squared times x squared divided by two minus m times g times x squared divided by two

Define the action:

cap s equals integral script cap l d t

Use variational principle

delta times cap s equals zero

to obtain the Euler-Lagrange equation:

d divided by d times t times open normal partial differential times script cap l divided by normal partial differential times x dot above close minus normal partial differential times script cap l divided by normal partial differential times x equals zero

Calculating separate terms:

equation sequence open d times s divided by d times t close squared equals x dot above squared plus y dot above squared equals x dot above squared times open one plus x squared close

equation left hand side normal partial differential times script cap l divided by normal partial differential times x dot above equals right hand side two times x dot above times open one plus x squared close

equation left hand side d divided by d times t times open normal partial differential times script cap l divided by normal partial differential times x dot above close equals right hand side two times x double dot times open one plus x squared close plus four times x times x dot above squared

equation left hand side normal partial differential times script cap l divided by normal partial differential times x equals right hand side two times x squared times x dot above squared plus two times omega squared times x minus two times g times x

Finally obtain the equation of motion:

x double dot times open one plus x squared close plus open g minus omega squared plus x dot above squared close times x equals zero

However, I am tempted to use an alternative method that I learned on my secondary school physics lessons. It is based on the direct application of Newtons laws and projecting vector equation equation left hand side m times a right arrow equals right hand side n ary summation over cap f right arrow on coordinate axes. Writing out the second law we have to bear in mind that the bead is acted upon by gravitational force and the force of normal reaction which arises due to Newton's third law and acts along the normal to the wire.

graph

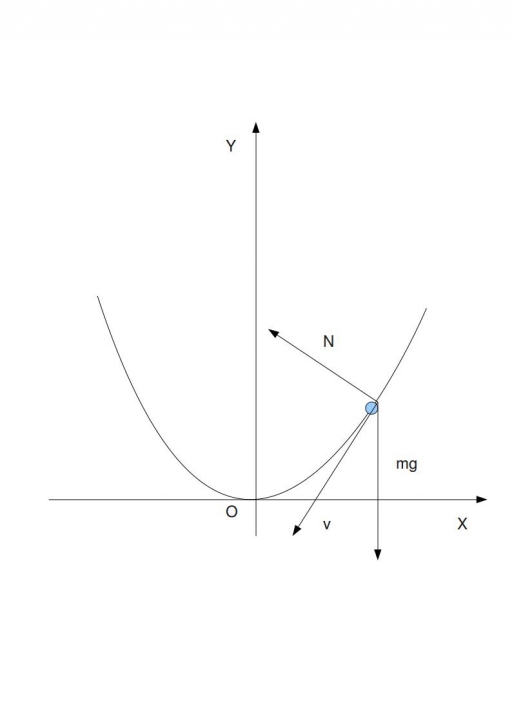
Hence Newton's second law is expressed as follows:

equation left hand side m times a right arrow equals right hand side m times g right arrow plus cap n right arrow

Acceleration is split into the tangential and centripetal parts:

equation left hand side a right arrow equals right hand side a right arrow sub tau plus a right arrow sub c

Projecting the equation on the vertcal axis we obtain:

equation left hand side m times a sub tau times sine of alpha plus m times g equals right hand side cap n times cosine of alpha

where alpha is the angle at which the tangent crosses the horizontal axis (hence tangent of alpha equals y dot above divided by x dot above )

Then project on the horizontal axis:

equation left hand side m times a sub c equals right hand side cap n times sine of alpha plus m times a sub tau times cosine of alpha

Eliminate cap n :

cap n equals m divided by sine of alpha times open a sub c minus a sub tau times cosine of alpha close

a sub tau times open sine of alpha plus cosine squared of alpha divided by sine of alpha close minus a sub c divided by tangent of alpha plus m times g equals zero

a sub tau divided by sine of alpha minus a sub c divided by tangent of alpha plus m times g equals zero

Now calculate the tangential acceleration:

equation sequence a sub tau equals d divided by d times t times open d times s divided by d times t close equals d divided by d times t times open Square root of x dot above squared plus y dot above squared close equals d divided by d times t times open x dot above times Square root of one plus x squared close equals x double dot times open one plus x squared close plus x times x two dot above divided by Square root of one plus x squared

and the centripetal part:

equation sequence a sub c equals omega squared times cap r equals omega squared times x

equation sequence sine of alpha equals one divided by Square root of one plus one divided by open y dot above divided by x dot above close squared equals y dot above divided by Square root of x dot above squared plus y dot above squared equals x times x dot above divided by x dot above times Square root of one plus x squared equals x divided by Square root of one plus x squared

equation sequence tangent of alpha equals y dot above divided by x dot above equals x

Plug the above results into the equation:

x double dot times open one plus x squared close plus x times x two dot above divided by Square root of one plus x squared times Square root of one plus x squared divided by x minus omega squared times x divided by x plus g equals zero

to obtain the same result

x double dot times open one plus x squared close plus open g minus omega squared plus x dot above squared close times x equals zero

Further analysis on the phase plane shows that when the wire rotates not very fast ( omega less than Square root of g ) the bead oscillates around the origin in the vertical plane. If omega greater than or equals Square root of g the bead is moving along the wire away from the origin, it's velocity tending asymptotically to value Square root of omega squared minus g

Tags: m821, dynamical systems
Permalink Add your comment
Share post

Comments

ND
Sunday, 16 Jan 2011, 08:24
by Niki Di Palma

New comment

Wah?