3.1 Fractions

The term ‘fraction’ means that a quantity is part of a whole, and is the result of dividing a whole amount into a number of equal parts. So, if you say that you can eat one-quarter of a pie, written as , then you are dividing the pie into four equal parts and saying that you can eat one of those parts. After you take your of the pie, three of the four quarters will remain, so the fraction remaining is three-quarters or . The numbers and are examples of fractions.

Fractions can be written in two different ways: three-quarters can be written as or 3/4. Both forms will be used in this activity. The first is used when writing out a calculation, but the second way is sometimes more convenient in a line of text.

Any fraction can be expressed in a variety of equivalent forms. Thus, two-quarters of a fruit pie, 2/4, means two of the four equal parts, and you know that this is the same amount as one half, 1/2. So 2/4 and 1/2 are said to be equivalent fractions because they are of equal value. Figure 3.1 shows four rectangular blocks of chocolate, of identical sizes, but divided into different numbers of equal-sized pieces. The darker areas can be expressed as different fractions, but all of the darker areas are the same size, so the four fractions are all equivalent. This means that:

In words, we would say ‘three-eighths equals six-sixteenths equals nine-twenty-fourths equals fifteen-fortieths’. Or an alternative way of saying this would be ‘three over eight equals six over sixteen equals nine over twenty-four equals fifteen over forty’.

Figure 3.1 Equivalent fractions of chocolate bars. The darker areas are all the same size.

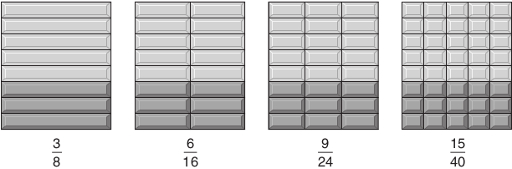
Note that you can change 3/8 to the equivalent fraction 6/16 by multiplying both the number on the top and the number on the bottom by 2. Similarly, you can convert 3/8 to 9/24 by multiplying both the top and the bottom by 3.

If you take any fraction, and multiply both the number on the top of the fraction and the number on the bottom by the same number – any one you care to choose – you will produce an equivalent fraction. Thus:

Here we have multiplied the top and the bottom of the fraction in turn by 2 (to get ), then by another 2, then by 5, and finally by 10.

Fractions are usually expressed with the smallest possible whole numbers on the top and the bottom. Working out the equivalent fraction with these smallest numbers is really a matter of finding numbers that can be divided into both the number on the top of the fraction and the number on the bottom. For example,

so these are all equivalent fractions.

Here we first divided the numbers on the top and the bottom of the first fraction by 10 to get , then we divided both numbers by 2 to get , and finally by 3 to end up with .

Note that all four of these fractions are equivalent, but we would normally use the fraction with the lowest numbers, .

Working out an equivalent fraction with the smallest whole numbers can be done step by step, as in the example above. It’s best to start by seeing if you can divide by simple numbers, like 10, 2, 5. Thus, if the numbers on the top and the bottom of a fraction both end in zero, then you can divide them both by 10 (first step in the example above). If they are both even numbers, then you can divide them by 2 (second step above). If both end in either a five or a zero, then they can be divided by five.

So, to express with the smallest whole numbers, you would divide the top and the bottom by 10. This division can be illustrated by ‘cancelling out’ the zeros by crossing them through with a diagonal line:

This cancelling process is the same as dividing – in this case dividing by 10. If there are more zeros, then more cancelling is possible. Thus:

Until now, we have only considered fractions for which the number on the top is smaller than the number on the bottom, so these fractions are part of a whole. However, it is possible to have a fraction in which the number on the top is larger than the number on the bottom, such as or , and these are sometimes called ‘improper fractions’. The fraction simply means five-quarters (of a pie, or whatever); only four-quarters can come from a whole pie, so the fifth quarter must come from another pie.