6 Measuring areas and volumes
6.1 Area
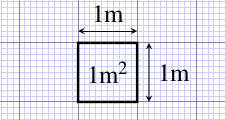
For squares and rectangles, the area is found by multiplying the length by the width. So a simple square with 1 m long sides (Figure 6.1) has an area of 1 m 1 m = 1 m2. In SI units, area is measured in square metres.
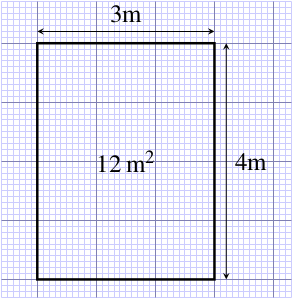
The rectangular garden pond shown in Figure 6.2 has an area of 3 m 4 m = 12 m2, and you can see that it is made up of 12 squares, each with sides 1 m long.
What is the area of a rectangular garden pond that measures 5 m 4 m?
The area is 20 m2.
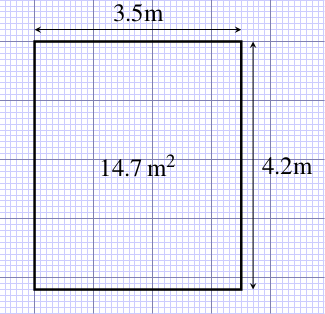
The rectangular garden pond shown in Figure 6.3 has an area of 3.5 m 4.2 m = 14.7 m2, which you can check with your calculator. The area is still the length multiplied by the width, and if you count up 12 whole squares and eight part squares you should be able to see that the pond covers the equivalent of about 15 whole squares, each of which has 1 m side length.
There are two ways of calculating the area of the L-shaped garden pond in Figure 6.4; can you see what these are?
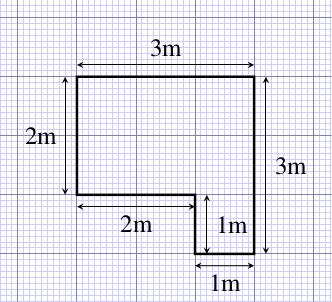Figure 6.4 Plan of an L-shaped garden pond.You could think of the pond as being a large rectangle, with a smaller rectangle taken out of it, as shown in Figure 6.5a. Or you could think of it as being made up of two rectangles, so that its total area is the sum of the areas of the two parts, as shown in Figure 6.5b.
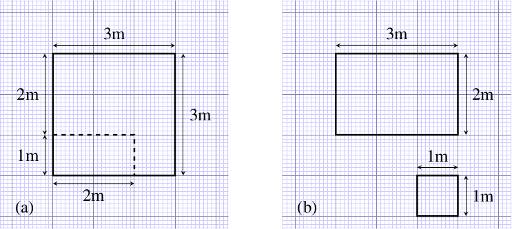Figure 6.5 Two ways of calculating the area of an L-shaped garden pond.
We can check that these two ways of calculating the area give the same answer.
Following the first method, in Figure 6.5a, the area is 3 m 3 m minus 2 m 1 m. Adding brackets to a problem of this type makes it look clearer and also emphasises the mathematical rule of carrying out the multiplication before the subtraction:
area = (3 m 3 m) – (2 m 1 m) = 9 m2 – 2 m2 = 7 m2
If you work this out on your calculator, brackets are not essential because your calculator follows the mathematical rules and will do the multiplication before the subtraction.
Following the second method, in Figure 6.5b, the area is 2 m 3 m plus 1 m 1 m, and again if we add brackets it makes the problem look clearer:
area = (2 m 3 m) + (1 m 1 m) = 6 m2 + 1 m2 = 7 m2
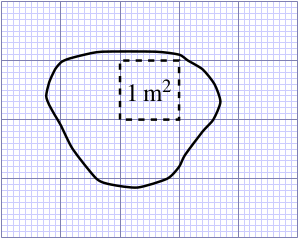
The concept of area is useful even for irregular-shaped objects; the irregular-shaped pond in Figure 6.6 has an area of about 5 square metres, and again you can verify this approximately, by counting up the metre squares and part squares.
