6.2 Volume
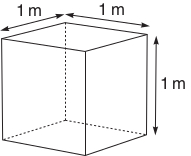
Volume is a measure of the space that a three-dimensional object occupies. The volume of a rectangular block is found by multiplying its length by its width by its height. A simple cube with 1 m long sides (Figure 6.7) has a volume of 1 m 1 m 1 m = 1 m3 (said as ‘metre cubed’ or ‘cubic metre’). In SI units, volume is measured in cubic metres.
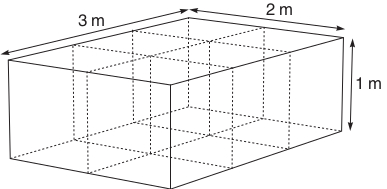
The fish tank shown in Figure 6.8 has a volume of:
3 m 2 m 1 m = 6 m3
and 6 cubes with 1 m sides could, in principle, be neatly stacked in the tank, as the dashed lines on the diagram indicate. For any rectangular block-like structure, such as a brick or a plank of wood, you can use the same method for measuring the volume: just multiply together the length, the width and the height, as we did for the tank in Figure 6.8.
Suppose you had measured the dimensions of a tank in centimetres, what would be the unit of its volume?
The unit would be cm cm cm, or cubic centimetres, which is abbreviated to cm3.
However, if you had measured one dimension in mm and the other two dimensions in cm, then before calculating the volume you would have to ensure all the dimensions were in the same unit.
What is the volume of a carton of fruit juice that has length 8 cm, width 45 mm, and height 12 cm?
Since 45 mm = 4.5 cm, volume of carton = 8 cm 4.5 cm 12 cm = 432 cm3.
Unless you’re in the building trade, you are probably not used to measuring volumes in cubic metres. A unit that is much more commonly used for measuring volumes of liquids is the litre (abbreviated to l). Fruit juices and emulsion paint, for example, are sold in litre volumes. A litre is the volume of a cube that has 10 cm sides.
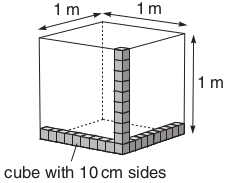
If you think about stacking cubes with 10 cm long sides in a 1 m cube (Figure 6.9), then you can see that we would need 10 10 10 = 1 000 of the 10 cm cubes to fill a cubic metre (1 m3), so
1 000 litres = 1 cubic metre (1 m3)
How many cubic centimetres (cm3) are there in 1 litre?
A cube with 10 cm sides has a volume of 1 litre. If you think about stacking 1 cm cubes in a 10 cm cube, then you can see that there are 10 10 10 = 1 000 of the 1 cm cubes in 1 litre, so 1 000 cm3 = 1 litre.
Question 6.1
A rectangular swimming pool has the following dimensions: 6 m long by 7 m wide and 2 m deep. What is the area of the bottom of the pool and what is the volume of the pool?
Area of the bottom of the pool is 6 m 7 m = 42 m2.
Volume of the swimming pool is 6 m 7 m 2 m = 84 m3.
Question 6.2
A reservoir is known to have the capacity to store 2.5 million litres of water. How many cubic metres is this?
Since 1 000 litres = 1 m3, then 2.5 million litres is