Personal Blogs

Consider the familiar square lattice. In principle it extends infinitely in every direction but the small patch below is enough to illustrate it. The distance between each point and its nearest neighbours could be anything, so let's just say it's 1 unit.

The question is whether we can embed a regular pentagon in this lattice so all its corners lie on lattice points. Is that possible? It could be any size and be slanted at any angle. Could a pentagon that fits the bill exist?

There's a clever but simple argument that shows the answer is no. Suppose we have three lattice points like for example ABC or A'B'C' in the next sketch.

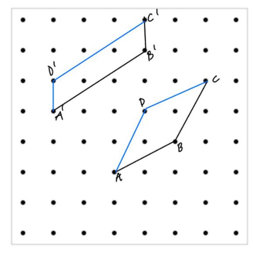
We observe that points such as D or D' that make a parallelogram with the original three points must always be lattice points too.

Now suppose we have a regular pentagon with corners that are lattice points. Its size doesn't matter, we are only saying its corners are lattice points.

Draw in the diagonals of the pentagon.

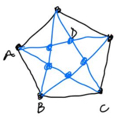
From what we said earlier, given that ABC are lattice points and ABCD is a paralellogram, point D must also be a lattice point. Working our way round the pentagon we see that all five blue points must be lattice points by the same reasoning.

These points form a regular pentagon, and so we have found a smaller pentagon which has its corners on lattice points.

But now we can repeat the process and find a still smaller regular pentagon all of whose corners are lattice points. We can repeat this indefinitely often, each time obtaining smaller and smaller pentagons whose corners lie on lattice points.

However this cannot be; eventually the length of the pentagon's sides would have to be less than 1 unit which is impossible, because 1 is the minimum distance between any two lattice points.

This means that if we could embed a regular pentagon in the square lattice we could go on to achieve something impossible. So embedding the regular pentagon must have been impossible in the first place.

This is my slightly adapted and I hope very slightly simpler solution to a beautiful question I found on Burkard Polster's Mathologer YouTube channel. In 'What does this prove?' posted July 25 2020 he uses animations to explore a series of related impossibility proofs, and discusses the history of several related problems. In particular he draws on an lovely blog post http://jdh.hamkins.org/no-regular-polygons-in-the-integer-lattice/