Apple are now selling motor vehicles, starting with something called the "iVan" but critics are sayings it's "terrible".
Personal Blogs
Not a lurid headline but a crossword clue, and the "calculating Swiss" is EULER, one of my heroes, pictured below in iconic headgear.

Leonhard Euler (1707-1783)
I was gratified to see that Euler has made it across into the realms of General Knowledge. There aren't many mathematicians famous enough for their name to be the answer to a Times Quick Cryptic Crossword clue.
The picture above, a pastel by Handmann painted in 1753, hangs in the Kunstmuseum Basel. This is probably the best known portrait of Euler.
Crossword Clue: "English" = E + "monarch" = RULER which "beheaded" becomes ULER, giving EULER (pro. "Oyler").
This was one of the first jokes I ever heard, in my infant school days.
When is a door not a door?
When it's ajar!
Yesterday I suddenly wondered, don't know why, where "ajar" comes from and what other things , if any, can be ajar (apart from a jar obviously).
The OED gives the definition "
Of a door, gate, or window: so as to be slightly or partially open.
It can apply to anything that closes off a space, so long as it's got hinges. The last bit is important, at least historically, because the original form was on char, where char means something like "turn". In Old English it was spelt in variety of ways, e.g. cyrre, chere, and referred at first to time "coming round". The meaning was extended to something physically turning; the OED gives this example from 1510
The dure on chare it stude.¶
So there we have our door. The meaning was then extended further to something like a "turn of work" — compare ways turn is used; take turns, it's your turn, etc. — and changed its spelling to chore, a piece of work that needs to be done. And so ajar and chore are related words, rather surprisingly.
But chare has left a fossil trace in the language, charwoman.
¶ Gavin Douglas, King Hart
I found this geometry problem at Cut the Knot
Euler Line Cuts Off Equilateral Triangle
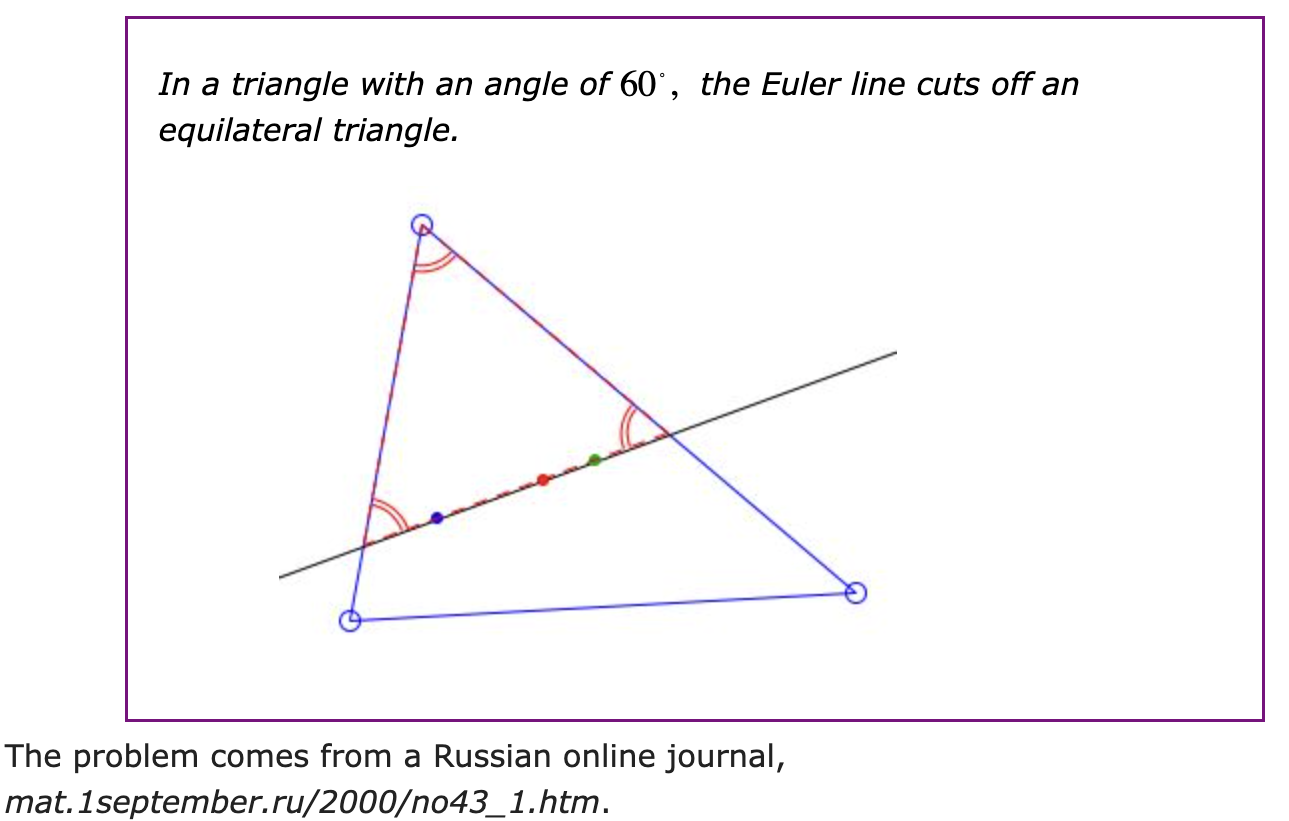
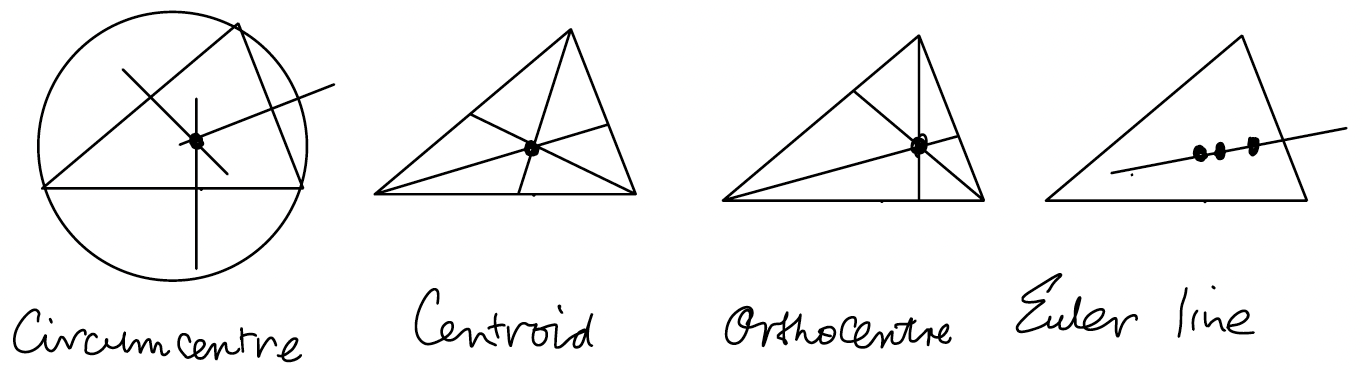
You probably need a bit of background. The Euler line is a line that passes through three of the four best-known triangle centres Although these centres were known to the mathematicians of Ancient Greece, this line was only discovered in 1765 by Leonhard Euler. My rough sketches below illustrate the three centres concerned and the Euler line.
 Our solution to the problem will use the following facts about the circumcentre and the centroid..
Our solution to the problem will use the following facts about the circumcentre and the centroid..
- The circumcentre is the centre of the unique circle, the circumcircle, that passes through the triangle's vertices.
- The centroid is the point where the triangle's medians meet. A median is a line joining a vertex of the triangle to the midpoint of the opposite side. The distance from a vertex to the centroid is twice the distance from the centroid to the corresponding midpoint.
- In an equilateral triangle the circumcentre and the centroid coincide,
Consider the following diagram.
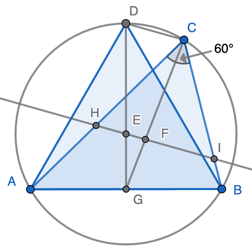
Triangle ACB is our 60° triangle. E is its circumcentre and F its centroid. Triangle ADB is an equilateral triangle inscribed in the circumcircle and on the same base AB. We can inscribe this triangle in the circle because any 60° angle subtended by AB must lie on the same circle. Because this triangle is equilateral the centre E is also its centroid, and GD a median.
Line HEFI passed through E the circumcentre of ACB and F its centroid, so it is the Euler line of ABC.
We note also that AD subtends angles ACD and ABD, so they both equal, and we know ABD is 60° because it is an angle of the equilateral triangle. Hence ACD is 60°.
Now the properties of medians come into play. DG is a median of the equilateral triangle ADB and E its centroid. Because of the properties of medians we have DG = 3EG.
Similarly CD is a median of our 60° triangle ACB and F its centroid and again using the properties of medians CG = 3FG
Now consider segment DC. Because DG = 3EG and CG = 3FG it follows that DC is parallel to the Euler line HEFI. Angles DCH and CHF are so-called "Z angles" on these parallel line, so they are equal, and we know already that DCH = DCA is 60°. So CHF = 60° also.
Now recall our problem. HEFI is the Euler line and we want to show it cuts off an equilateral triangle. HCI is 60° by assumption, and we have just shown a second angle CHI in the triangle that is cut off is also 60°. But that means all three angles of triangle CHI must be 60° and it is equilateral as claimed.
PS I've not read the solution(s) given on Cut The Know because I wanted to find my own proof but I'm going to take a look now.
The Language-Lover's Lexipedia, by Joshua Blackburn. I learned of this wonderful book via the podcast and YouTube channel Words Unravelled, and it is an absolute joy.
The breadth and depth of Mr Backburn's research and scholarship are simply stunning, but at the same time he manages to maintain a light and playful tone. To give a flavour of the book here's a potted version of just one of the 200+ entries, from Abracadabra to Zyzzyva.
 We've all heard of the Bee's Knees and the Cat's Pyjamas I suppose, and perhaps also the Duck's Quack, although that's less familiar. But until now I never real stopped to wonder where they came from. Turns out they were Flapper slang.
We've all heard of the Bee's Knees and the Cat's Pyjamas I suppose, and perhaps also the Duck's Quack, although that's less familiar. But until now I never real stopped to wonder where they came from. Turns out they were Flapper slang.
When I think about Flappers I have a hazy vision of the Roaring Twenties and bobbed hair style and the Charleston and all that sort of thing. Merriam-Webster's more informed definition is " a young woman predominantly of the 1910s and 1920s who showed freedom from conventions (as in style of dress and conduct)".
And they also had their own Flapper-Speak which included a craze for phrases consisting of the name of an animal followed by something mildly surprising or incongruous (the Duck' Quack is an outlier here). Mr Blackburn has dug up a whole bunch of examples, forgotten now apart from the three I gave above. Here are some of my favourites:
The Bullfrog's Beard
The Clam's Garters
The Eel's Ankle
The Hen's Eyebrows
The Kipper's Knickers
And if you fancy a Bee's Knees cocktail Mr Blackburn has found the recipe.
Picture credit: Copilot 27 November 2025
A million thanks to New Scientist magazine (Feedback 22 October 2025) for alerting me to the (serious, I promise) scientific paper by Paul Silvia and Meriel Burnett entitled,
What’s brown and sticky? Peering into the ineluctable comedic mystery of dad humor with a handful of machine learning models, hundreds of humans, and tens of thousands of dad jokes *
As well as the paper, the website hosts a downloadable list of, as promised, 32,000 jokes. The download is Joke Database.zip, just over 50 MB. When expanded it holds two datasets, one with the full 32k jokes (all gathered from Reddit) and the other a subset of 501 jokes the researchers put to a panel of human joke evaluators.
I was able to open the big dataset in Excel ¶ and sure enough it is a treasure house of (slightly over) 32k (mostly) family-friendly dad jokes. Just imagine, a dad joke a day for almost 90 years.
The database contains a lot of data beyond the actual jokes and would be fertile ground for further research or so I imagine. But for now I thought I would come up with a program to print random dad jokes on request.§ Here's a sample run, as you'll see the jokes are of variable quality.
See a random joke? y/n y
A burglar broke into our house last night and stole all of the light bulbs I should be upset, but I'm delighted.
See a random joke? y/n y
I was really mad when they locked me in a room with nothing but the remnants of a dead chicken, but I got out. Good thing I had a bone to pick.
See a random joke? y/n y
What do you call someone who does not like physics A physicist .
See a random joke? y/n y
My Llama roommate yelled at me, "I've had enough of your dad jokes! Leave now!" "Fine," I replied, "Alpaca my bags and leave."
See a random joke? y/n y
Why are almost all (capital) Greek letters old? Because there is only one Greek letter that is new (N/v). &#;
See a random joke? y/n y
The cashier at the grocery store asked "paper or plastic?" I said "paper" thinking she meant "cash or charge." She started bagging my stuff in a paper bag so I yelled: "No! Plastic." Then she screamed at me: "Hey! we don't...take...Credit Cards."
See a random joke? y/n y
what do the eiffel tower and a tick have in common? they are both "parisites" lol
See a random joke? y/n n
* Published on OSF Oct 29, 2025, 12:27 PM.
¶ Be warned, the spreadsheet has a lot of columns.
§ Python code below:
import csv, random
jokes = []
with open("Reddit_Dad_Jokes_OSF.csv", mode='r', encoding='utf-8') as file:
reader = csv.reader(file)
for row in reader:
jokes.append(row[1])
quit = False
while not quit:
resp = input("See a random joke? y/n ")
if resp == "y":
print(random.choice(jokes))
print()
else:
quit = True
A phonestheme is when a large number of words that start with the same sound (most typically a consonatn pair) to have related meanings. The phenomenon was first noted by J. R. Firth in 1930. A classic example is fl-, which I remember being fascinated by when first reading about it. Here are some words beginning with this consonant pair fl-.
flit, flash, flutter, flung, flicker, flee, flip, flap, flare, flurry, fly, flow
What all these have in common is some notion of movement, especially sudden or repetitive movement.
The Wikpedia article gives a number of other examples, such as cl-, e,g. clop, clap, cling, clasp, clutch, all to do with moving an object; and sn-, e.g. snort, snitch, snot, snout, snivel, snitch, sneeze, sniff, sneer, snore, snorkel, all nose-related.
So is there some real effect here, is there something inherently fluttery about fl-? If so, is there some deep psychological connect? Or it it mimetic; does "flutter sound like something fluttering? Or is it somehow to do with how we make a "fl" sound, do we flap our tongue when we pronounce it? (probably not). And then we know from historical evidence that words can influence other similar sounding words, so that could be at work too.
Is there even enough statistical evidence to support the idea that fl- carries a semantic load? Perhaps we are just (as people do) see in a pattern because we always look for them?
We might be able to provide some evidence by doing some clever statistical analysis, but it's slippery (there's another example of a phonestheme, sl-; slip, sled. slop, slime slither, slobber, sludge). But what criteria do we use to decide of a word belongs in the list? Should slow be counted? What about slag? Slant? Sleet? Slick?
I tried some rough experiments with the help of Copilot. It says
About 8–10% of common English words starting with “fl” relate to repeated or sudden movement.
Is that evidence. Well maybe. We'd have to come up with some list of representative and comparable (how to define what these mean?) semantic fields and see if 8-10% was unusually high.
Another of the examples in the Wikipedia articles is gl-, which is connected with shining or gleaming etc. I discussed this in a previous post A Little "Eggymology" and it is very likely to be a real connection but one that is simple to explain. The words probably all share an etymology and are descended from a PIE root *ghel-, "shining". So no profound mystery. This time Copilot tells me 6-7%. If the proportion for fl- words sharing the same semantic field is higher than that for gl- where (we think) an effect is known to exist what does that tell us? (But I haven't checjed Copilots findings.)
Another example quoted is stand, stable, state, stasis, but from memory this too is a group of words thought to have a common ancestry, a PIE root *sta-, "stand" or something like that.
So is a phonestheme a real thing? It's an intriguing concept, but the jury is still out. There seems to be a school of thought that believes it is just an illusion, but it seems too tat there are also serious scholars and ongoing research in support of there being something real in the idea. Either way I find it fascinating.
In this proof of the puzzle discussed here we drop some perpendiculars, which is often a good start in Euclidean style geometry problems.
 |
Given a square ABCD, if a diagonal be drawn from B to D and another line drawn from A to the midpoint E of CD, so as to intersect the diagonal at F, the triangle formed by the two lines and the base AB of the square is one third of the square. Proof: We can take the side of the square to be 1, so its area will be 1. Construct perpendiculars EJ from E to BD, FH from F to AB, and FI from F to DA. Let the distance from A to H be d. Then the angles of AIFH are all right angles, so it is a rectangle, and side FI which is opposite to AH must also have length d. The point F lies on the diagonal BD, which bisects the angle at D, and therefore the perpendicular distances FI and FG are equal, and FG has length d also. Triangles AJI and AHF are similar, because they share a common angle FAH and both have a corresponding right angle. The distance JI is 1 and the distance AJ is .§ Therefore the ratio of EJ to AJ is 2:1 and that of FH to AH the same. The length of AH is d and there FH must be 2d. Then we have HG = 2d + d = 3d, and HG = 1 so FH = 2d = . The area of the shaded triangle AFB is base x height = x x 1 = , as claimed. |
§ We should probably prove this, which is easy enough but clutters uo the proof a bit.
This puzzle was posted on Twitter by Ed Southall of Huddersfield University§§ back in 2018 and quickly went viral.
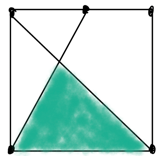
What fraction of the square is shaded? (The line from the bottom left corner needs the top side of the square at its midpoint).
This question attracted a lot of media attention. As the Daily Mail put it, “Tricky maths problem sweeping social media leaves many scratching their heads”. However it passed me by at the time, and I only saw it last weekend, so here are my two takes at it. I haven't looked at any of the many solutions on the internet, but I my guess is the reasons why it has been so popular are
- The problem is easy to understand
- It's not trivial to solve
- But there are lots of different solutions.
Take #1
My first idea is shown in the sketches below.
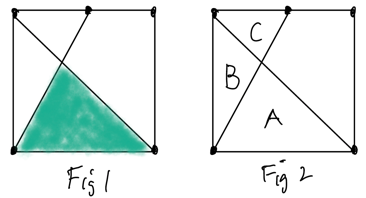
Suppose the three triangles have areas A, B and C as shown in Figure 2. Then the three "look and see" dissections in Figures 3-5 let us write down three equations. (Figure 3 is a bit ropey but hopefully you get the idea.)
We have three equations in three unknowns and it's fairly easy to solve them.
From Figure 3, B = ½ - A.
From Figure 5, C = ¼ A.
Plug these into the equation illustrated by Figure 4.
½ - A + ¼ A = ¼, multiplying by 4 gives 2 - 4A + A = 1, 1 = 3A and so A is
Take #2
But then I though, if A is made up of 4 small triangles, what if we superimpose a triangular grid on the whole square? I drew this in Geogebra.
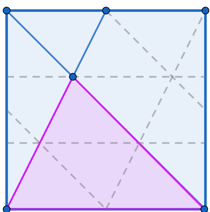
Eureka! See what happens if we shift the leftmost triangle by half the length of the square's side to the right.
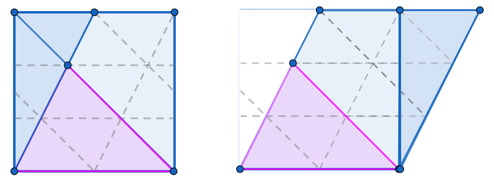
The area has not changed and we can now see that it is equal to that of 3 rows of 4 = 12 of the small triangles. The area the puzzle asks for is 4 of these small triangles, so it is = of the area of the square.
egg is from Middle English, from Old Norse, replacing an earlier English word ey. Both are of Germanic origin but probably go back to a PIE root *owyo-, which also gave us Latin ovum and Ancient Greek oon, as well as cognates in other languages. Intriguingly there is even a hint of a connection with *awi- "bird" and perhaps even further back to a word that meant "clothed" (birds are clothed in feathers , you see).
yolk is from yellow, OE geolu + a suffix which might be -ca, a diminutive (so "small yellow") or -ock, or something else: there seems no general agreement. And yellow? It is probably from a PIE root *ghel-, "shining", and so perhaps connected with gleam and glisten and a number of other words starting with gl- and semantically related to brightness or shining.
Here is an interesting Old English passage from Aelfric's Catholic Homilies, about 990 CE, in which he uses the analogy of an egg to how how two distinct things can be part of a single whole.
Sceawa nu on anum æge, hu þæt hwite ne bið gemengd to ðam geolcan, & bið hwæðere an æg.
"Look now at an egg, how the white is not mixed with the yolk, and yet it is one egg." (Chat GPT 5)
"There is a tavern in the town, in the town
And there my dear love sits him down, sits him down
And drinks his wine 'mid laughter free,
And never, never thinks of me."
When I first visited Greece and went to a taverna I thought that name might be a borrowing from English. After all Greek has a word "bar". But in fact both languages have borrowed from Latin, Greek directly and English via French (and now again from Greek, so taverna is now an English word too).
The Latin taverna seems to have been something like a shop/stall/shed/tent, with connotations of being moveable. A related word is tabernacle, used in the English translation of the Bible to mean a moveable sanctuary or temple, and deriving from the diminutive form tabernaculum, "tentlet" (the suffix is the same as in pendulum, "little hanging thing").
Other related words are architrave, where the -trave element is from an Italian words for beam and the unusual word contubernal, "living in the same tent". More surprisingly there may just be an ancient connect with tree, which may originally meant "beam" or "dwelling". You can see the semantic connection.
Imagine three fair spinners.
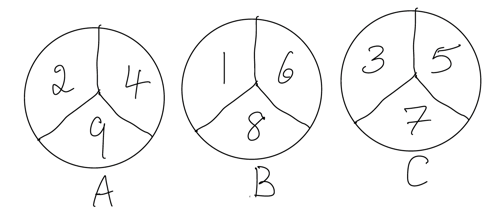
If we compare A and B there are 9 equally likely outcomes. The ones where A wins are highlighted.
2-1 2-6 2-8 4-1 4-6 4-8 9-1 9-6 9-8
A beats B 5/9 or about 56% of the time.
if we compare B with C there are 9 equally likely outcomes. The ones where B wins are highlighted.
1-3 1-5 1-7 6-3 6-5 6-7 8-3 8-5 8-7
B beats C 5/9 or about 56% of the the time.
So A beats B most of the time and B beats C most of the time. How will A fare against C? Intuitively we might reason A beats B and B beats C, so A will beat C most of the time too. But not so! C beats A the majority (56% again) of the time. Here's C versus A, C's wins highlighted.
3-2 3-4 3-9 5-2 5-4 5-9 7-2 7-4 7-9
This is a simplified version I made up of something called intransitive dice (Wikipedia), where three dice are numbered in such a way that A will beat B the majority of the time, B will beat C the majority of the time, but when A is pitted against C it is C that has the greater chance of winning. It's also possible to have a longer chain, of four or more dice.
Interesting
If we arrange the numbers 1 through 9 into a 3x3 square and note which numbers are on spinners A, B and C, we find we hey a "Latin square"; each letter appears in each row and each column,
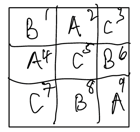
Also note the three numbers on any spinner always sum to 15.
Just for fun I wrote and ran a Python simulation that spins the three spinners a million times and prints out the percentage of the time A beats B, that B beat C and that C beats A, and sure enough I got
A>B 55 %
B>C 56 %
C>A 56 %
Program below
import random
A = [2, 4, 9]
B = [1, 6, 8]
C = [3, 5, 7]
abeatsb = 0
bbeatsc = 0
cbeatsa = 0
trials = 1000000
for go in range(trials):
a = random.choices(A,k=1)[0]
b = random.choices(B,k=1)[0]
c = random.choices(C,k=1)[0]
if a > b:
abeatsb = abeatsb + 1
if b > c:
bbeatsc = bbeatsc + 1
if c > a:
cbeatsa = cbeatsa + 1
print('A>B',round(abeatsb/10000),'%')
print('B>C',round(bbeatsc/10000),'%')
print('C>A',round(cbeatsa/10000),'%')
Good news! I’ve taught my dog to beg. It’s about time he helped pay the bills.
When I came to this crossword clue —
Small crown for one in farewell (5)
— I wondered where "tiara" comes from.
Everywhere I looked agreed it is from Latin tiara, which was in turn a borrowing from Greek, but it's not clear if we can trace it back further. The OED describes it as being "of unknown origin" and Wiktionary likewise, but Etymonline suggests the Greek word is "of Oriental origin". Geoffrey Munn, quoted in Wikipedia, suggested the word is from Persian and was applied to the crown worn by Persian kings. It was indeed, but I'm not sure we can infer from this that the word was Persian.
My doubt arise from the fact that Munn also mentions diadems as being wrapped around said tiaras.
This is also true, but diadem is pure Greek; it has a Greek meaning, something like 'around binding'. The OED explains its etymology in this way, and describes it as "the regal fillet of Persian kings" (which I rather like) and states that Alexander the Great adopted it in the course of his conquests. So the headgear was indeed Oriental but the name used for it by Greek writers was a Greek one.
So we have no real evidence for "tiara" being of Persian origin that I can see; the Greek may have borrowed it from somewhere else, or it might have been pre-Greek, or it might have Greek etymology now lost to us.
So my quest for the origin of "tiara"only took me so far and I think the OED's conclusion that the Greek word τιάρα is of unknown origin is sound.
In 1685 the mathematician John Wallis recounted that Prince Rupert had a bet that it is possible to pass a cube through a hole in one of smaller side length. Wallis showed how this could be done and out ot curiosity I tracked dow the source in the Internet Archive. Here it is

I only know odd words of Latin, so I asked Copilot what this was (that's all I asked, I gave no clues apart from the image) and quite surprisingly it not only read the text and translated it but also identified what it was and meant.
Copilot
The image contains a Latin excerpt from John Wallis's work on Prince Rupert's Problem, a famous geometric puzzle. Here's a translation and explanation of the key parts:
📜 Latin Text (Translated)
Prince Rupert, while at the court of King Charles II of England, a man of great ingenuity and insight, claimed—and said he would demonstrate—that it is possible for one cube to pass through a hole in another cube of equal size. He was said to have actually done this. We will now show how this can be done.
🧩 Problem Statement
Problem:
Of two equal cubes, shape one in such a way that the other, intact, can pass through it.
Wallis' diagram shows the view from one corner of the cube looking towards the opposite corner and inside it a square with side length equals to that of the cube's faces, showing a cube of the same size could indeed pass through.
But this is not the best possible solution! A century later Peter Nieuwland found it is actually possible to pass a bigger cube through, which I posted about three or four years ago. His solution is known to be the best possible.
The problem remained a curiosity until the 1960s, when it was found you can have a "Prince Rupert's Tetrahedron" and a "Prince Rupert's Octahedron", and then it was found the other two Platonic Solids also work, although physical models twould be very hard to make because the size differences are very small.
There was then speculation that all convex (roughly, no sticky-out bits. dimples or holes) polyhedra might be "Rupert". However the breaking news is that this conjecture isn't true! A convex polyhedron has just been found that isn't Rupert. There is a really good article here
https://www.quantamagazine.org/first-shape-found-that-cant-pass-through-itself-20251024/
Own work
Septentrionate means "To point North", ultimately derived from Latin septentrio, "North". You have probably spotted the first element sept- is connected to the number seven. the second part, trio, is not to do with three, but apparently mean "plough ox". So what were these seven plough oxen? Well here they are:

A familiar constellation in the Norther sky, Ursa Major and often also called The Big Dipper/The Plough/Charles' Wain.
Latin also had Boreas, the North wind originally and I think borrowed from Greek (think Aurora Borealis). Modern Greek for North is still βορράς, voras, so it hasn't changed much, except that the letter beta has become a "b" sound to a "v" sound in Modern Greek.
I leaned that Septenrio was Latin for North from the excellent Words Unravelled podcast and YouTube channel, which also featured the surprising fact that Romance languages have names for North, South, East and West that are essentially the same as the English words, e.g French nord, sud, est, and ouest. This is as a result of borrowing, most likely from Old English into Old French and from there to the other languages, supplanting the names inherited from Latin.
It's not at all clear why this replacement happened. When I heard about it I assumed that the geographical closeness of France to England and of Spain, Portugal, Italy to France would have been a factor, but to my astonishment I found Romania shares the borrowing too, even though it's much further off. So it's a mystery.
And where did North come from anyway? Well not everyone agrees with it, but the strongest theory is that the word and its cognates in other Germanic languages come from a root that meant "left" (or perhaps "down" or both). Why would North be left? Because most ancient societies, would probably have been East oriented (literally), rather than North because that is where the Sun rises, and when we look East, where is North then?
I bought some vegetables and the packet said wash before eating, so I went upstairs and took a quick shower.
This is the solution to the puzzle at https://learn1.open.ac.uk/mod/oublog/viewpost.php?post=312323
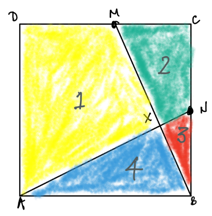
Given ABC is a square of area 100 sq. units and M and N the midpoints of the sides on which they lie, to find the areas 1, 2, 3 and 4.
Solution
The small triangle (3) can be got from triangle (4) by a rotation of 90° followed by a scaling. The hypotenuse of triangle (4) is equal to the side length of the square, and that of triangle (3) is half the side length of the square, so the dimensions of (3) are half those of (4) and its area one-quarter the area of (4).
But (3) and (4) between them make up one-quarter of the square, which represents an area of 25 sq. units and given their areas are in the ratio 1:4 the area of (3) must be 5 sq. units and that of (4) 20 sq. units.
The combined areas of regions (2) and (3) is also one-quarter of the square, hence the area of region (2) must also be 20 sq. units.
Finally the areas of these three regions add up to (20 + 5 + 20) sq. units, which leaves 55 sq. units for region 1.
So finally we have
Region 1: 55 sq. units
Region 2: 20 sq. units
Region 3: 5 sq. units
Region 4: 20 sq. units

The square has an area of 100 sq. units and points M and N are the midpoints of the sides they lie on. Lines AM and BN cut the square into four regions numbered 1, 2, 3 and 4 as shown. Find the area of each of these regions.
Answers tomorrow.
I saw this on a YouTube channel "Knights & Knaves" but this or similar questions seem to have been asked elsewhere too.
In a circle, if we draw 10 random chords, what is the expected number of times two of the chords will intersect?
(What we mean by a random chord needs defining but for the purposes of this question we take it to be that each chord joins two points on the circumference with a uniform probability distribution, so the probability of the point chosen lying in a given arc is the length of that arc as a proportion of the circumference.)
One solution begins with the case of two chords and reasons along these lines. Suppose we choose four random points and consider the point A. If we join it randomly to one of the other points there are three cases, as shown below, and they are all equally likely, with probability 1/3.
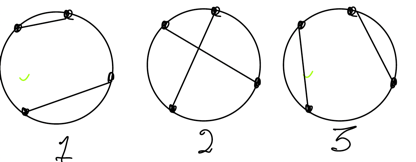
Cases 1 and 3 have no intersections, Case 2 has 1. So the expected number of intersections is
(1/3)x0 + (1/3)x1 + (1/3)x0 = 0 + 1/3 + 0 = 1/3
This seems to be the generally accepted argument, but I felt it was rather glib, so I got Copilot to write a simulation in Python. You can find the program at the end of this post. I added a bit of code at the end to run it multiple times and after 10,000,000 trials the overall proportion of times it found an intersection was 33.34%, so that seems to support the expectation being 1/3.
The argument continues as follows. We know the expectation for one pair of chords is 1/3 and if there are 10 chords there will be "10 choose 2" which is 10x(10-1)/2 = 45. There is a beautiful fact, called Linearity of Expectation, which tells us if the know the individual expectations of a set of random variables we can find their combined expectation just by adding all the individual expectations together, and this is valid even if the random variables are not independant of one another.
So in the present case we just add 45 lots of 1/3, one for each pair of chords, and find the expected number of intersections is 15. In the general case of n chords we have "n choose 2" pairs, and the expected number of intersections is nx(n-1)/2 lots of 1/3, or nx(n-1)/6.
I think this is the standard line of argument and there is no need to consider how many pairs there are. Here is a simpler approach that occurred to me.
Suppose we have two chords c1 and c2 and we add a third, c3. The expectation that c1 intersects c2 is 1/3 and the expectations that c3 intellects c1 and c2 are 1/3 and 1/3 respectively. By the Linearity of Expectation we can just add all these, so we get 1/3 + 1/3 + 1/3 = 1.
Now if we add a fourth chord c4, the expectation of it intersecting c1, c2 and c3 respectively will all be 1/3 so now the total expectation is 1 + 3x(1/3) = 2. When add a fifth chord the expectation will be 2 + 4x(1/3) = 10/3, and so on. After we have added the n-th chord the total expectation will be
(1 + 2 + 3 +... + (n-1)) x (1/3) = ((n-1)xn/2) x (1/3) = nx(n-1)/6
and voilà, we have the same answer as before!
Here is the Python program generated by Copilot
import math
import random
def generate_random_point_on_circle():
angle = random.uniform(0, 2 * math.pi)
return (math.cos(angle), math.sin(angle))
def ccw(A, B, C):
"""Check if three points are listed in a counter-clockwise order."""
return (C[1] - A[1]) * (B[0] - A[0]) > (B[1] - A[1]) * (C[0] - A[0])
def segments_intersect(A, B, C, D):
"""Return True if line segments AB and CD intersect."""
return ccw(A, C, D) != ccw(B, C, D) and ccw(A, B, C) != ccw(A, B, D)
def random_chords_intersect():
# Generate two chords
A = generate_random_point_on_circle()
B = generate_random_point_on_circle()
C = generate_random_point_on_circle()
D = generate_random_point_on_circle()
# Check if they intersect
return segments_intersect(A, B, C, D)
count = 0
trials = 10000000
for trial in range(trials):
if random_chords_intersect():
count = count + 1
print((count/trials)*100)
Thanks to those excellent people at Merriam-Webster you can now travel back in time to see what words and expressions are first attested from any particular year. It's interesting to see what words have become common, which are around but not common, and which have faded from view.
Here are some from 80 years ago, first some that are fairly familiar today (I couldn't find an example for all 26 letters) and don't all seem as old as they are, then some that are now obscure (to me anyway).
- anti-fungal, blip, commoner, d'oh, end user, firestorm, guided missile, hassle, information theory, macroeconomics, name-dropping, off-limits, press-secretary, rollover, snorkel, turbocharged, up-front, work ethic
- acrocentric, bacitracin, daidzein, extraliterary, infraorderer, microbus, nol-pros, ripstop, scungilli, vizsla, x-height
A customer walks into a pet shop and asks to buy a giraffe. "Hey, that's a tall order", says the shopkeeper.
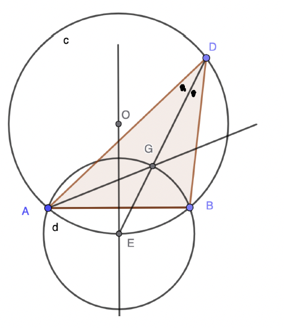
In the diagram above circle c is the unique circle passing through the vertices of triangle ABC (its circumcircle) and the line through O and E bisects the side AB at right angles (the perpendicular bisector of AB). The perpendicular bisector intersect the circumcircle at point E.
1) What is special about the line ED?
Every point on the perpendicular bisector is necessarily equidistant from A and B, so AE is equal to EB. Equal chords on the same circle make (subtend) equal angles on the circumference of that circle, and so ∠ ADE and ∠ EDB are equal, as shown. We see that ED is the angle bisector of ∠ ADB. I presented thois rather neat result in an earlier post.
2) As noted E is equidistant from A and B and we can therefore draw a circle d, centred at E, that passes through A and B, as seen in the diagram above. What is the significance of the point G at which the angle bisector ED cuts this circle and what is the line AG that also passes through G?
In the figure below we have shown an addition line segment EB (dotted).
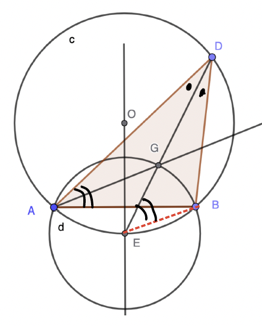
A classic theorem well known to Euclid tells us that in a given circle any two angles subtended by the same chord are equal. In circle c, ∠ BED and ∠ BAD are both subtended by chord BD, so they are equal, as shown.
Next we consider the angles in circle d. In the diagram below we have shown the segment BE (dotted), which is a chord of circle d.
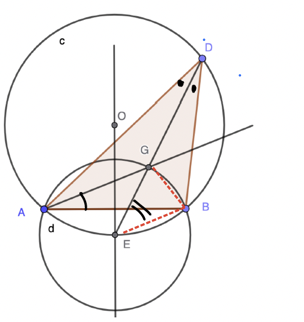
A second classic theorem, also familiar to Euclid, stated that the angle a chord subtends at the centre of a circle is twice the angle it subtends at any point on the circumference of that circle. In circle d chord BG subtends ∠ BEG at the centre and ∠ BAG at the circumference. Hence∠ BEG = 2 ∠ BAG, or ∠ BAG = ½ ∠ BEG = ½ ∠ BAG because we already know ∠ BEG, which is the same as ∠ BED, is equal to ∠ BAD.
Thus we see that GA bisects ∠ BAD and is a second angle bisect, and G the point at which the two angle bisectors meet. But it is well known that all three angle bisectors meet at a single, point called the incentre, which is the centre of the unique incircle, the circle inside the triangle that is tangent to all three of its sides.
Conclusion
In a triangle the perpendicular bisector of a side and the angle bisector of the angle opposite that side meed at a point on the triangles circumcircle which is the centre of a circle passing through the vertices of that side and also through the incentre of the triangle.
All this is building up to a very beautiful theorem proved by Euler, which connects the radii of the circumcircle and the incircle with the distance between their centres. That's for another post.
30 September, 2025
Anglesey has what may be the finest display of cyclamens in the country, rivalled only by the RHS gardens at Wisley.
 The name cyclamen goes back to Greek kyklos, "circle", and we have related words like circus and cycle etc. These words may even be related to ring, the common PIE root being something like *sker-, "turn", with kyklos being a reduplicated form skersker. "ring" is from the same PIE root, so I suppose "circus ring" could be consider a triplication.
The name cyclamen goes back to Greek kyklos, "circle", and we have related words like circus and cycle etc. These words may even be related to ring, the common PIE root being something like *sker-, "turn", with kyklos being a reduplicated form skersker. "ring" is from the same PIE root, so I suppose "circus ring" could be consider a triplication.
But what has this to do with cyclamens? Well the plant grows from a round tuber and the plant is named for that, the theory goes. This seems a bit tenuous to me; many plants have round tubers or bulb or corms, so why are cyclamens special?
This blog might contain posts that are only visible to logged-in users, or where only logged-in users can comment. If you have an account on the system, please log in for full access.