This is a Sangaku-like puzzle (see https://learn1.open.ac.uk/mod/oublog/viewpost.php?post=230691)
We have a square inscribed in a triangle of known base b and height h, as shown. What is the length s of the square's side?
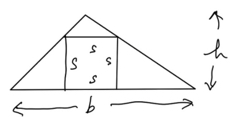
I called this a Samurai puzzle because many of the original sangaku were the work of Samurai.
(Solution in Comments.)
Comments
One Solution
A solution
I thought of this question last night and it took me quite a while to find a solution that I felt had the simplicity of the problem itself; for example with no trigonometry as in sin, cos, tan or even Pythagoras; or coordinate geometry. In the style that Euclid would have used perhaps.
Surprisingly (to me anyway) the square has the same side length for every triangle with the same base and height, whatever its angles are.
New comment
Although Euclid wouldn't have used b and h etc. but labled the points A, B, C and so on and named the lengths AB and so on, and no brackets or modern notation, so much longer to write but the same thoughts.