While I was having my dinner this puzzle occurred to me.
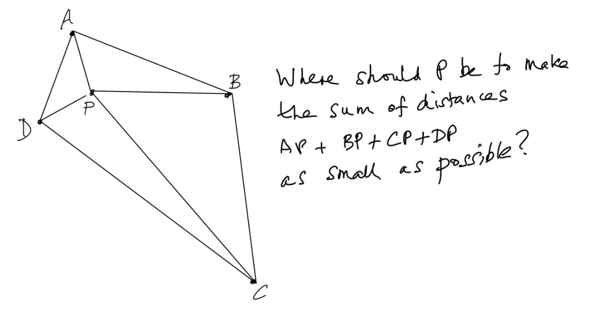
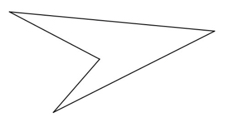
Assume the quadrilateral is convex, and has no re-entrant corners of the sort shown in this example.
After a bit of sketching quadrilaterals and points, I saw what the really beautiful answer is. Scroll down to read more.
.
.
.
.
.
.
.
.
.
.
.
.
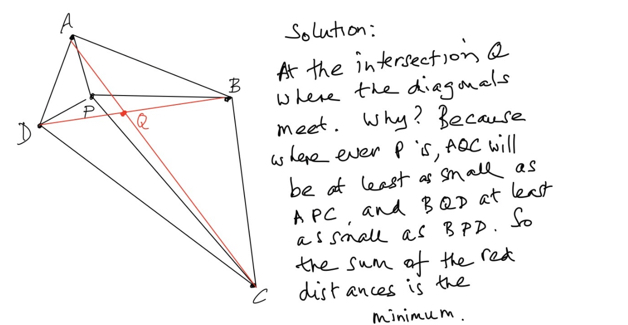
Then I went off to do some research, and of course there is nothing new under the sun. Fagnano wrote about this question ca. 1750. But similar questions still arouse research interest. Suppose we had different ways of measuring distance? Or we weren't on a flat surface? Or what about 4 points in space? Or more than 4 points in the plane?
Comments
New comment
Hi Richard,
My instinct told me to join opposite corners and the intersection is on the shortest path for all points to the centre. Then as I scrolled down...
As a current MST124 student, it looked vaguely similar to something a Unit or two back
Jan