Another puzzle I found on John Baez's blog. It seems to have been discovered and published only as recently as 2011. Baez's post gives a reference.
Two touching semi-circles, aligned as shown, are inscribed in a circle.
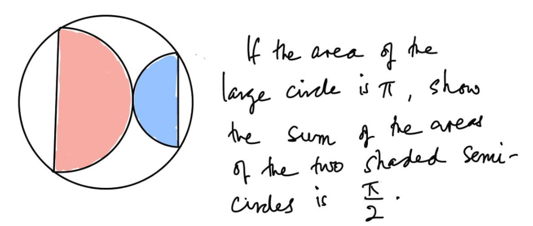
You might think you need more information, such as the relative sizes of the semi-circles perhaps. But in fact it doesn't make any difference.
I will post my solution on 6 March.
Comments
New comment
IF you maximise the red semicircle and minimise the blue semicircle,
THEN you end up with a semicircle that has its straight side as the diameter of the outer circle.
THEREFORE Therefore the total of the 2 semicircles covers half the area of the outer circle.
Jan (who has time now to catch up on blogs after submitting MST124 TMA03 6 days early )
)
New comment
That's true Jan but it only works given my statement that the relative sizes are irrelevant, i think you need to prove this fact before you can say the solution is complete 🙂
New comment
Hi Richard,
I'm being lazy today. I think I'll wait until I see your solution
Jan