Personal Blogs

Some more geometry! 

We can inscribe a square in an equilateral triangle so that all itas corners lie on the sides of the triangle. How? Well, consider this sketch.

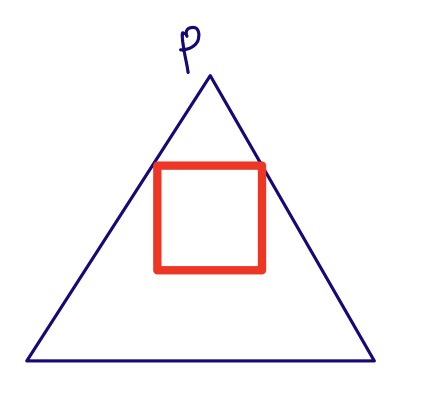
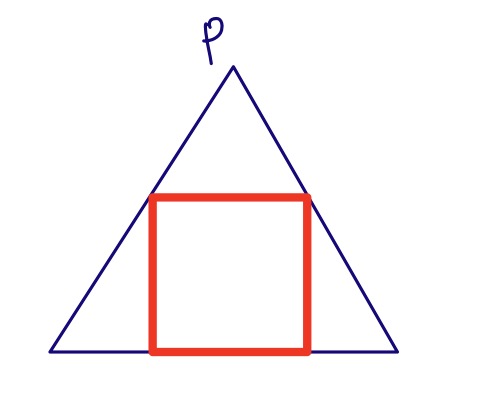
We draw a chord of the triangle parallel to the base and draw a square with the chord as one of its sides. Then we move the chord vertically downwards, keeping it parallel to the base and with its ends on the sides of the triangle and progressively enlarging the square, until the base of the square lands on the base of the triangle, and we are done.

We can extend the idea to three dimensions and inscribe a cube in a regular tetrahedron.

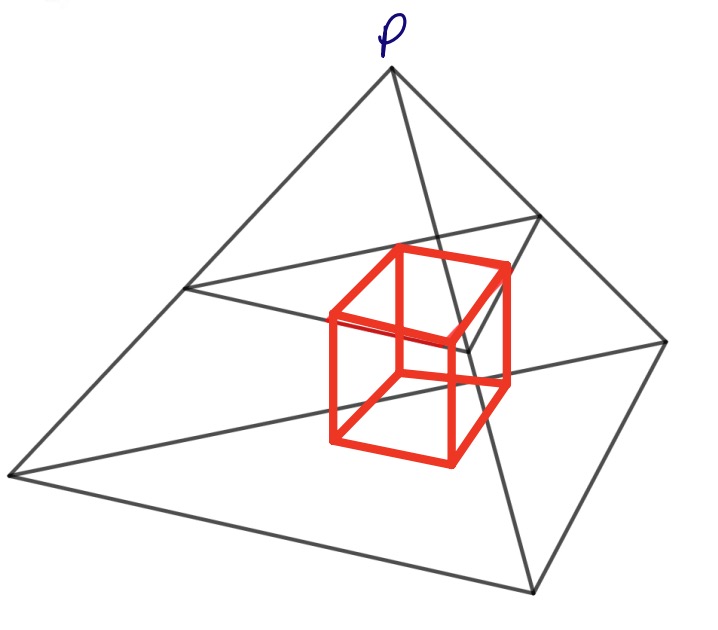
We take a section parallel to the base and in this equilateral triangle inscribe a square using the method described above, and construct a cube with this square as one of its faces. Then we move the section vertically downwards, keeping its vertices on the sides of the tetrahedron, progressively enlarging the cube, until the base of the cube lands on the base of the tetrahedron, and we are done.

It's conjectured, but I don't think proved, that this gives the largest cube that can be inscribed in a regular tetrahedron, see here.

Rather neat, and It seems to me that an analogous construction would be possible in dimension and beyond, a hypercube in a 4-simplex and so on, but I can’t prove it and drawing a picture of even the four dimensional case feels quite a challenge.