On this 10 x 10 square grid I have drawn some rectangles with their corners on points of the grid and their sides parallel to the sides of the square. The colours have no particular significance I just used them to make the picture more interesting.
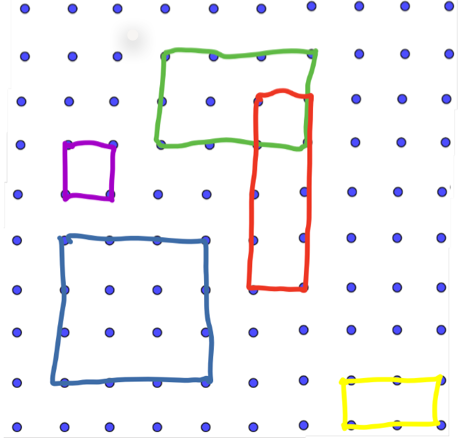
There are obviously many other rectangles that can be drawn on this grid. Can you work out how many there are altogether? Answer on Tuesday.
Comments
New comment
A physicist's solution (relying more on algebra than geometry):
An rectangle can be placed in possible locations, and we have space for any rectangle size from to . So we can write the total number of rectangles as
.
Multiplying out the brackets,
.
Now we can use the fact that and (both of which can be calculated easily by hand) to write
.
All terms but the last cancel, and we are left with
.
New comment
Great answer Steven, there are indeed 2025 possible rectangles, which I thought was rather neat!
This is also the sum of the cubes 13 + 23 +... + 93, another fun fact.