While I was having my breakfast I found this Geometry Proof on Instagram.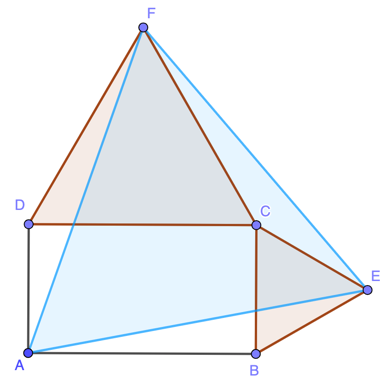
On two adjacent side of rectangle ABCD draw equilateral triangles CFD and BEC as shown. Prove the triangle AEF is equilateral.
Presh Talwalkar solved this by constructing some right-angled triangles and applying Pythagoras and algebra to show all three sides have equal length.
I approached the proof differently, without Pythagoras or any significant algebra. I'll put my solution in the Comment later on today.
Comments
New comment
New comment
I got there the same way that you did 😊
I haven't looked at the other solution yet.
Jan
New comment
The other way is relatively straightforward but we have to fiddle around with the distances and bring in the square root of 3, so it's a bit messy and to my mind not so insightful.
Interesting Footnote
The circle through the centres of the three equilateral triangles has a radius equal to that of the large equilateral triangle's circumcircle. This circle also passes through the apexes of the two smaller triangles and is tangential to the sides of the large triangle at those points.
New comment
Very elegant 😊
Jan
New comment
Yes it is very neat and it's just something I spotted when playing around with the diagram in GeoGebra.