This puzzle was about situating three ranger stations in a wildlife park with a square boundary in a way that is in some sense optimal.
One solution partitions the park into three regions and positions the ranger stations so that (1) each station has oversight of the same area, (2) each point on the park is overseen by its nearest station, and the maximum the distance between any station and a point in its region of responsibility is smaller than if we simply divided the park into three rectangular strips in the obvious way.
However if we are prepared to compromise over either (1) or (2) the maximum distance of travel can be further reduced.
In the arrangement above the side of the square is s and the other distance are as shown. The dotted lines are diameters of the regions and are all of length . The ranger stations are at the midpoints of the diameters (blue dots) and the further distance of travel ever needed is ≈ 0.504s.
By suitably choosing the distance HP we can equalise the areas, or we can have every point overseen by the nearest station, but we cannot achieve both these objectives simultaneously. Although this problem is obviously highly idealised, it occurred to me in real life situating strategic resources must often involve this type of compromise.
"The Three Ranger Stations" revisisted
This puzzle was about situating three ranger stations in a wildlife park with a square boundary in a way that is in some sense optimal.
One solution partitions the park into three regions and positions the ranger stations so that (1) each station has oversight of the same area, (2) each point on the park is overseen by its nearest station, and the maximum the distance between any station and a point in its region of responsibility is smaller than if we simply divided the park into three rectangular strips in the obvious way.
However if we are prepared to compromise over either (1) or (2) the maximum distance of travel can be further reduced.
In the arrangement above the side of the square is s and the other distance are as shown. The dotted lines are diameters of the regions and are all of length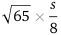
. The ranger stations are at the midpoints of the diameters (blue dots) and the further distance of travel ever needed is 
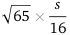≈ 0.504s.
By suitably choosing the distance HP we can equalise the areas, or we can have every point overseen by the nearest station, but we cannot achieve both these objectives simultaneously. Although this problem is obviously highly idealised, it occurred to me in real life situating strategic resources must often involve this type of compromise.