Suppose we have a long piece of wood with a uniform cross-section which is an irregular triangle (Fig. 1), so a straight cut at right angles to the length of the timber results in a triangle all of whose sides are different.
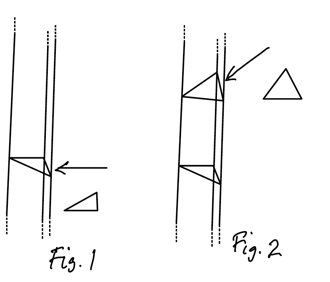
Show that it is always possible to make an oblique cut at an angle in such a way that the section obtained is an equilateral triangle (Fig. 2).
This comes from the Turkish Maths Olympiad 2000 and I read about it here, p. 141.
An outline proof appears in the comments.
Comments
New comment
Here's a sketch of how the proof works, illustrated by a particular triangle , but the idea will apply generally. I've presented it in six stages.
Stage 1: as an example suppose the straight cross section of the timber os a triangle with sides 3, 4, and 5. Imagine irt drawn on graph paper, so the vertices A, B and C have the coordinates shown.
Stage 2: now we are going to make a cut at an angle, so we introduce a third coordinate to represent height. We leave point A at height 0 and let P and Q stand for the heights pf B and C.
Stage 3: we want a section that is an equilateral triangle, so we require the lengths AB, BC and CA to be equal. Using the standard formula for distances between points in three dimensions gives the system of equations shown.
Stage 4: the equations have two solutions, but they are not essentially different and I just picked one arbitrarily.
Stage 5: these are the three dimensional points we get.
Stage 6: checkin that all three distance are the same, and they are.
You might wonder if this has solved the problem, can we make a plane cut through these three points, and the answer is yes , we assuredly can, because any three general points in three dimensions alway lie on a unique plane.
To answer the Olympiad question properly we'd need to work with general points and not actually solve the equations but discuss their solution. But what I've written above is the gist of the proof and I think it's rather nice problem.