I got this rather nice problem from Cut the Knot, and it was originally from the Leningrad Maths Olympiad.
Can we visit each of the 8 vertices of a cube exactly once and return to the starting vertex by following a path made up of 8 straight line segments, each connecting a vertex of the cube to another of the cube's vertices?
The answer is yes and below we see one possible solution, with the dotted path meeting the these conditions.
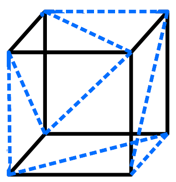
However you will notice that in this tour 3 of the segments coincide with edges of the cube. Is it possible to find such a path where none of the segments coincide with an edge?
Prove that the answer is no, no such path can exist.
Solution in comments.
Comments
Proving it's impossible.
A straight line that joins two vertices of a cube but isn't an edge must be a diagonal: either a diagonal of one of the cubes face's or a "space" diagonal joining two diametrically opposite corners.
The two vertices of a given face intersect, so only one of them can be on the path.
The three space diagonal intersect at the cube's centre, so only one of them can be on the path.
So the maximum number of diagonals the path can have is one per face, giving 6, plus 1 space diagonal, making 7 altogether.
But the path has 8 segments, so there are not enough diagonals to go round and at least one segment has to be an edge.