Every now and again someone comes up to me in a pub or a hotel or a classroom and sketches this little picture.
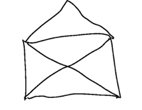"Can you draw this", they say, "without going over the same bit twice or lifting the pen off the paper?"
"I can", I say, and then I try to explain how I can be so confident without even picking up the pen. Here's how it goes.
First identify each point where two of more lines meet.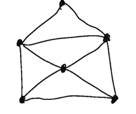
Now count how many lines meet at each point.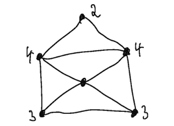 
For it to be possible to trace the figure it's necessary that either:
- All the numbers are even, or;
- Two and only are odd (as is the case here) and you start from one of these and end at the other.
This is because every time you pass through a point you add 2 to the count. If you start and finish at the same point then an extra 1 is added when start and another 1 again when you finish, so all the counts are even. Otherwise if we start and finish at different points, both get an extra 1, so their final count will be odd but all the other counts even.
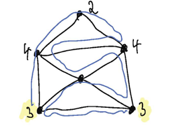
Providing one of these holds it can be proved (but I'm not going do so here, it's not that hard but a bit too long) that the figure can be traced. And here's a solution (not the only one). The points with an odd count are highlighted.
These ideas were first articulated by Leonhard Euler in 1736. A problem that must have been going the rounds at the time concerned the seven bridges of Königsberg (in Prussia then; now Kaliningrad in Russia). The puzzle was: is it possible to find a tour that crossed each bridge exactly once.
Here are the bridges as shown in Euler's original paper, which you can find in translation here.
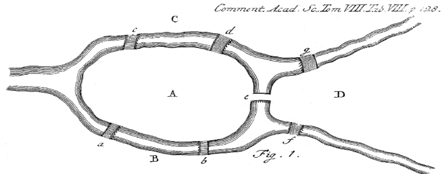
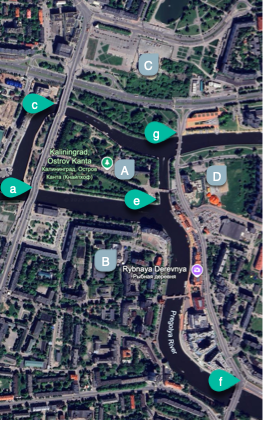
Out of interest I looked for the bridges on Google Earth and as you can see only five are still there; b and d were presumably destroyed in WW II. I hope I have identified the other five correctly.
Now if we take A, B , C and D to be points, and the original seven bridges a - g as lines connecting the points, we get this figure, and the problem of the Königsberg bridges becomes one of tracing the figure without crossing any bridge twice or taking the pen off the paper.
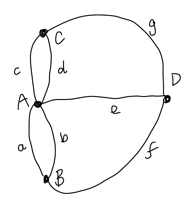
All four of A - D have an odd number of lines meeting at them, so from the discussion given earlier the puzzle of the seven bridges has no solution, although with only the five bridges that have survived it does become possible to make a tour of the desired kind, starting at A and ending at D, or vice versa.
Euler called his paper, which has since become very famous, "SOLUTION OF A PROBLEM IN THE GEOMETRY OF POSITION" and it gave rise to the branch of mathematics now called graph theory: nothing to do with x and y-axes, or plotting lines and parabolas etc., but concerned with the properties of arrangements consisting of points (vertices) connected by lines (edges). As well as being of great intrinsic interest and beauty, graph theory is a vital tool in the design of the algorithms and data structures behind the computer programs that play such an important role in modern life.