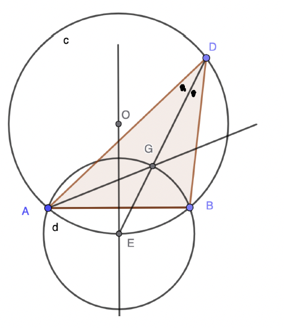
In the diagram above circle c is the unique circle passing through the vertices of triangle ABC (its circumcircle) and the line through O and E bisects the side AB at right angles (the perpendicular bisector of AB). The perpendicular bisector intersect the circumcircle at point E.
1) What is special about the line ED?
Every point on the perpendicular bisector is necessarily equidistant from A and B, so AE is equal to EB. Equal chords on the same circle make (subtend) equal angles on the circumference of that circle, and so ∠ ADE and ∠ EDB are equal, as shown. We see that ED is the angle bisector of ∠ ADB. I presented thois rather neat result in an earlier post.
2) As noted E is equidistant from A and B and we can therefore draw a circle d, centred at E, that passes through A and B, as seen in the diagram above. What is the significance of the point G at which the angle bisector ED cuts this circle and what is the line AG that also passes through G?
In the figure below we have shown an addition line segment EB (dotted).
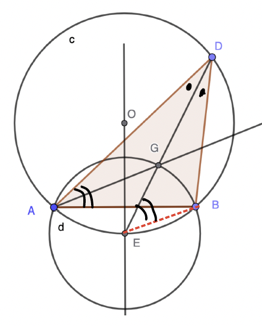
A classic theorem well known to Euclid tells us that in a given circle any two angles subtended by the same chord are equal. In circle c, ∠ BED and ∠ BAD are both subtended by chord BD, so they are equal, as shown.
Next we consider the angles in circle d. In the diagram below we have shown the segment BE (dotted), which is a chord of circle d.
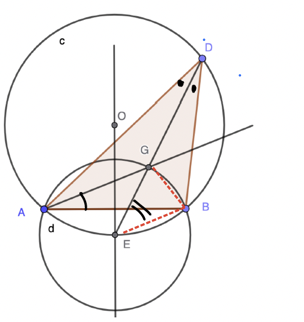
A second classic theorem, also familiar to Euclid, stated that the angle a chord subtends at the centre of a circle is twice the angle it subtends at any point on the circumference of that circle. In circle d chord BG subtends ∠ BEG at the centre and ∠ BAG at the circumference. Hence∠ BEG = 2 ∠ BAG, or ∠ BAG = ½ ∠ BEG = ½ ∠ BAG because we already know ∠ BEG, which is the same as ∠ BED, is equal to ∠ BAD.
Thus we see that GA bisects ∠ BAD and is a second angle bisect, and G the point at which the two angle bisectors meet. But it is well known that all three angle bisectors meet at a single, point called the incentre, which is the centre of the unique incircle, the circle inside the triangle that is tangent to all three of its sides.
Conclusion
In a triangle the perpendicular bisector of a side and the angle bisector of the angle opposite that side meed at a point on the triangles circumcircle which is the centre of a circle passing through the vertices of that side and also through the incentre of the triangle.
All this is building up to a very beautiful theorem proved by Euler, which connects the radii of the circumcircle and the incircle with the distance between their centres. That's for another post.