This puzzle was posted on Twitter by Ed Southall of Huddersfield University§§ back in 2018 and quickly went viral.
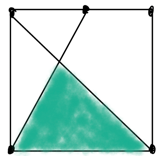
What fraction of the square is shaded? (The line from the bottom left corner needs the top side of the square at its midpoint).
This question attracted a lot of media attention. As the Daily Mail put it, “Tricky maths problem sweeping social media leaves many scratching their heads”. However it passed me by at the time, and I only saw it last weekend, so here are my two takes at it. I haven't looked at any of the many solutions on the internet, but I my guess is the reasons why it has been so popular are
- The problem is easy to understand
- It's not trivial to solve
- But there are lots of different solutions.
Take #1
My first idea is shown in the sketches below.
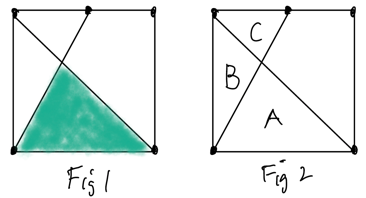
Suppose the three triangles have areas A, B and C as shown in Figure 2. Then the three "look and see" dissections in Figures 3-5 let us write down three equations. (Figure 3 is a bit ropey but hopefully you get the idea.)
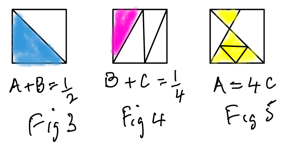
We have three equations in three unknowns and it's fairly easy to solve them.
From Figure 3, B = ½ - A.
From Figure 5, C = ¼ A.
Plug these into the equation illustrated by Figure 4.
½ - A + ¼ A = ¼, multiplying by 4 gives 2 - 4A + A = 1, 1 = 3A and so A is
Take #2
But then I though, if A is made up of 4 small triangles, what if we superimpose a triangular grid on the whole square? I drew this in Geogebra.
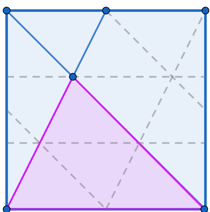
Eureka! See what happens if we shift the leftmost triangle by half the length of the square's side to the right.
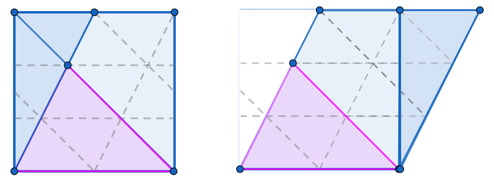
The area has not changed and we can now see that it is equal to that of 3 rows of 4 = 12 of the small triangles. The area the puzzle asks for is 4 of these small triangles, so it is = of the area of the square.