Problem 1358 at gogeometry [1] asked for a proof that in a regular 12-sided polygon the four diagonal shown all meet at a point. This is quite surprising; it\'s not hard to find threee diagonals the meet at a single point but four is rarer.
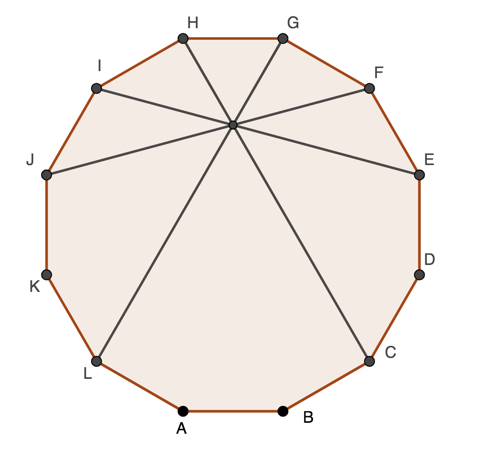
After playing arouind for a while I found a proof which was reasonably neat, but I had to use sines and cosines at one point, and I'd hoped for something simpler; and there was nothing very illuminating about my proof in any case. Stan Fulger came up with something much more insightful. Here is his beautiful answer.
It uses two well-known facts about triangles.
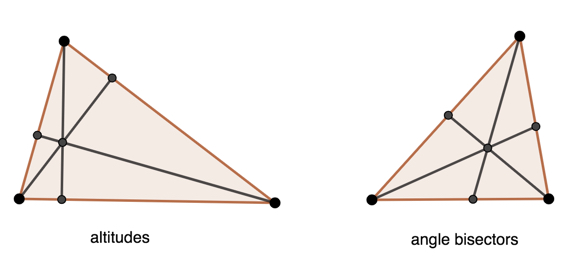
The altitudes of a triangle, i.e. the lines drawn from each vertex at 90° to the opposite side, meet at a point.
The angle bisectors of a triangle, i.e. the lines which divide each angle in half, meet at a point.
For example
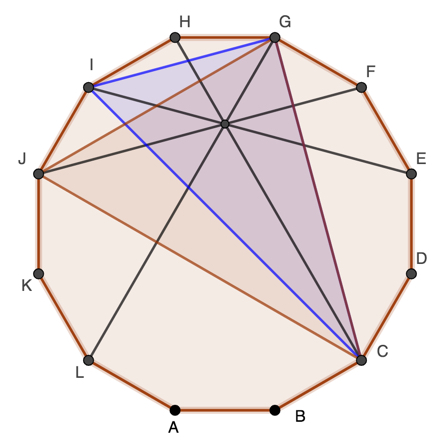
Now for a "look and see" proof.
In the picture below three diagonals are angle bisectors in the blue triangle, so they meet at a point. Also three diagonals are altitudes of the orange triangle and therefore meet at a point. Two of the diagonals are both a bisector in one triangle and an altitude in the other. Therefore all four diagonals meet at a point.
I drew the figures above using GeoGebra classic.
[1] Geometry problem 1358 https://gogeometry.com/school-college/4/p1358-dodecagon-regular-concurrency-diagonal-infographic-classes.htm