I found this geometry problem at Cut the Knot
Euler Line Cuts Off Equilateral Triangle
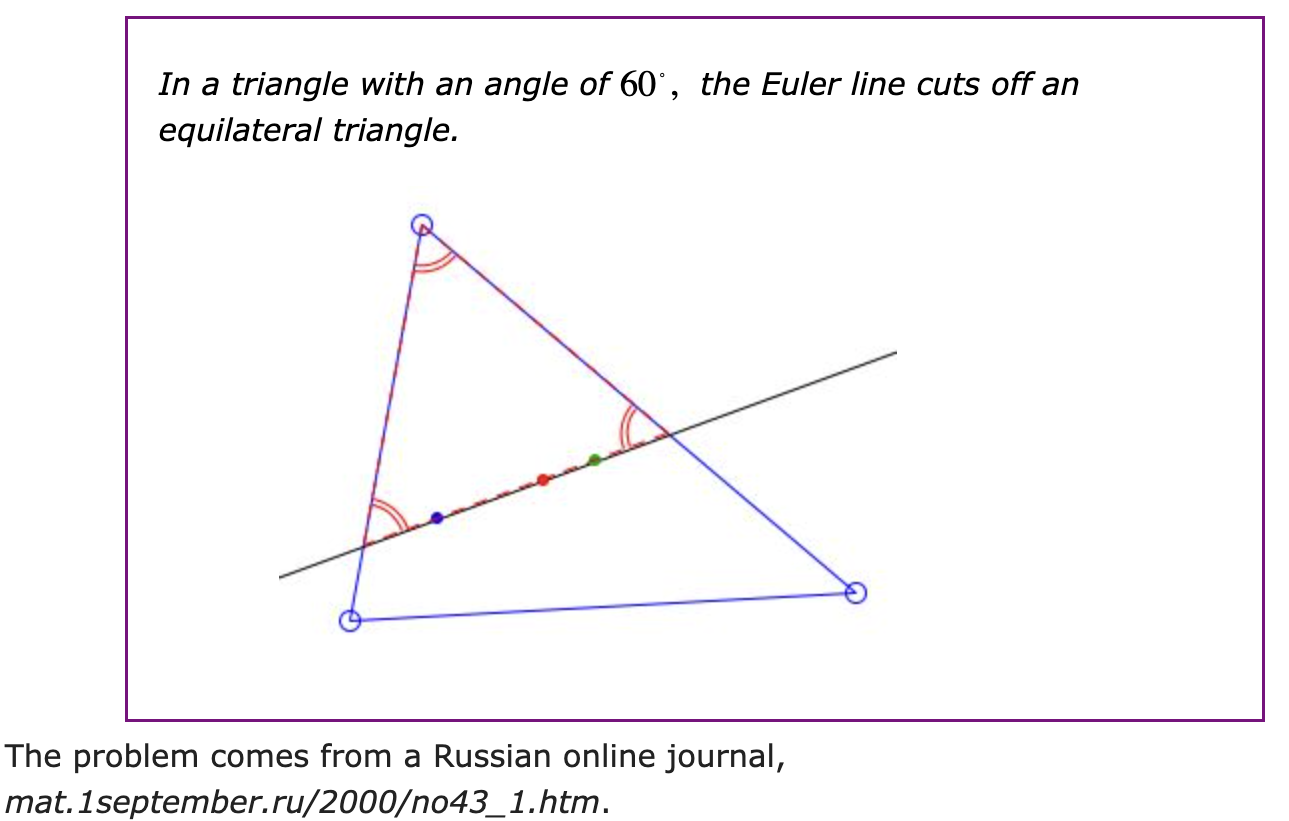
You probably need a bit of background. The Euler line is a line that passes through three of the four best-known triangle centres Although these centres were known to the mathematicians of Ancient Greece, this line was only discovered in 1765 by Leonhard Euler. My rough sketches below illustrate the three centres concerned and the Euler line.
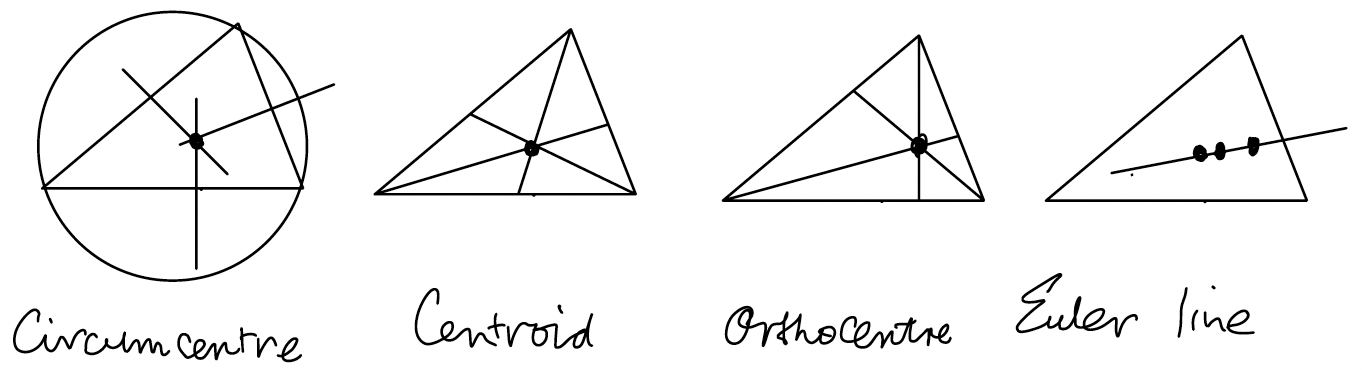Our solution to the problem will use the following facts about the circumcentre and the centroid..
- The circumcentre is the centre of the unique circle, the circumcircle, that passes through the triangle's vertices.
- The centroid is the point where the triangle's medians meet. A median is a line joining a vertex of the triangle to the midpoint of the opposite side. The distance from a vertex to the centroid is twice the distance from the centroid to the corresponding midpoint.
- In an equilateral triangle the circumcentre and the centroid coincide,
Consider the following diagram.
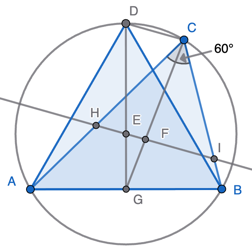
Triangle ACB is our 60° triangle. E is its circumcentre and F its centroid. Triangle ADB is an equilateral triangle inscribed in the circumcircle and on the same base AB. We can inscribe this triangle in the circle because any 60° angle subtended by AB must lie on the same circle. Because this triangle is equilateral the centre E is also its centroid, and GD a median.
Line HEFI passed through E the circumcentre of ACB and F its centroid, so it is the Euler line of ABC.
We note also that AD subtends angles ACD and ABD, so they both equal, and we know ABD is 60° because it is an angle of the equilateral triangle. Hence ACD is 60°.
Now the properties of medians come into play. DG is a median of the equilateral triangle ADB and E its centroid. Because of the properties of medians we have DG = 3EG.
Similarly CD is a median of our 60° triangle ACB and F its centroid and again using the properties of medians CG = 3FG
Now consider segment DC. Because DG = 3EG and CG = 3FG it follows that DC is parallel to the Euler line HEFI. Angles DCH and CHF are so-called "Z angles" on these parallel line, so they are equal, and we know already that DCH = DCA is 60°. So CHF = 60° also.
Now recall our problem. HEFI is the Euler line and we want to show it cuts off an equilateral triangle. HCI is 60° by assumption, and we have just shown a second angle CHI in the triangle that is cut off is also 60°. But that means all three angles of triangle CHI must be 60° and it is equilateral as claimed.
PS I've not read the solution(s) given on Cut The Know because I wanted to find my own proof but I'm going to take a look now.