Here is my solution to the Japanese Temple Problem (Sangaku) I posted here a couple of days ago.
The problem ask for the radius of the small green circle in Figure 1 below, assuming the radius of the largest circle is 1 unit.
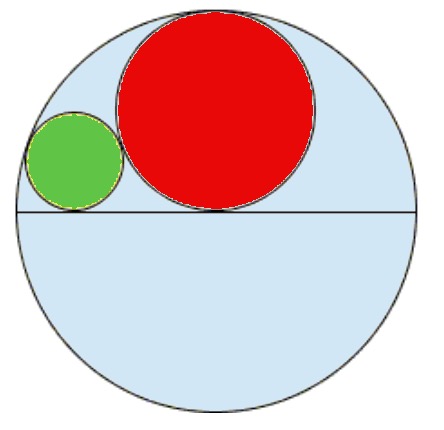
Figure 1. Sangaku problem
Figure 2 shows the construction, which is followed by the explanation.
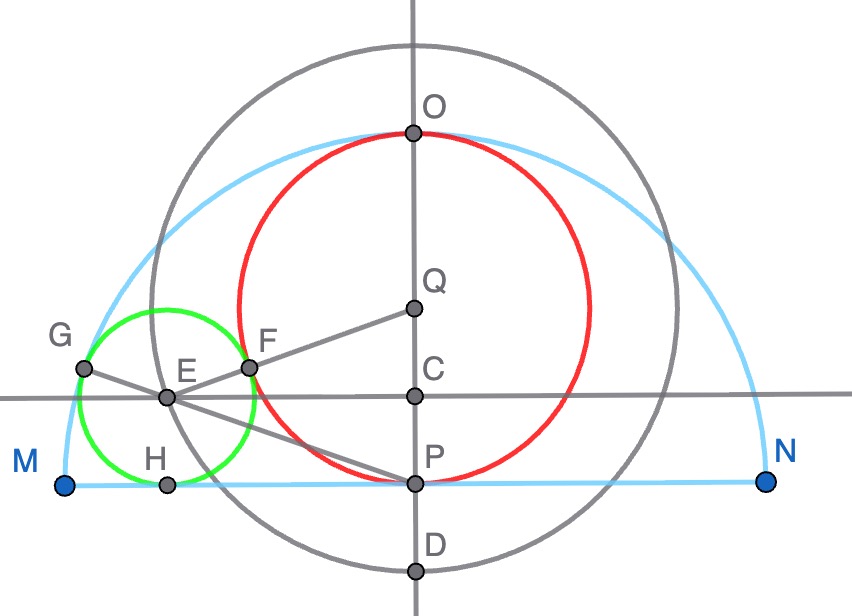
Figure 2. The construction
Explanation
O and P are respectively the points at which the red circle is tangent to the blue semicircle and its diameter MN. Q is the centre of the red circle.
Draw a line bisecting PQ at right angles. The distance CP is and the perpendicular distance between any point on the bisector and the diameter MN must therefore also be .
Next draw a circle with centre Q and radius to intersect the bisector of PQ at E. Now draw the green circle with centre E and radius .
To show this is the required circle we need to show it is tangent to the diameter, the red circle and the semicircle.
Because the radius of the green circle is \(\frac{1}{4\}) and that is also the distance between the bisector and the diameter, the green circle and the diameter must be tangent at H.
Because the distances QE and FE are and by the construction and QF by assumption, QE = QF + FE and so the red and green circles are tangent at F.
Because CE is the perpendicular bisector of PQ, PE= QE = , PG must pass through E, and PG = OE + EG = + = . G therefore lies on the circumferences of the blue and green circles and must be the point at which the are tangent.
The answer to the problem is therefore , a very neat result.