I am posting it in reply to a question I came across in one social network. There is no original material here. I am just trying to reproduce the argument from one university lecture, as far as I can remember it.
The task is to calculate optimal stock level at a warehouse. Stock is replenished to a certain value (which is to be determined) immediately at fixed equally spaced moments in time. Amount of stock units cnosumed during each period is random.
Let be the stock level which is maintained. Assume that stock is replenished over a fixed period of time (take it to be unitary to simplyfy calculations). Assume that units are used during each time period with probability .
Let be unitary storage cost, is a “penalty” cost
assigned when stock is theoretically below 0, or below some
minimal admissible level (lost orders, emergency orders, etc).
Assume also that the stock is replenished immediately.
Consider two possible situations.
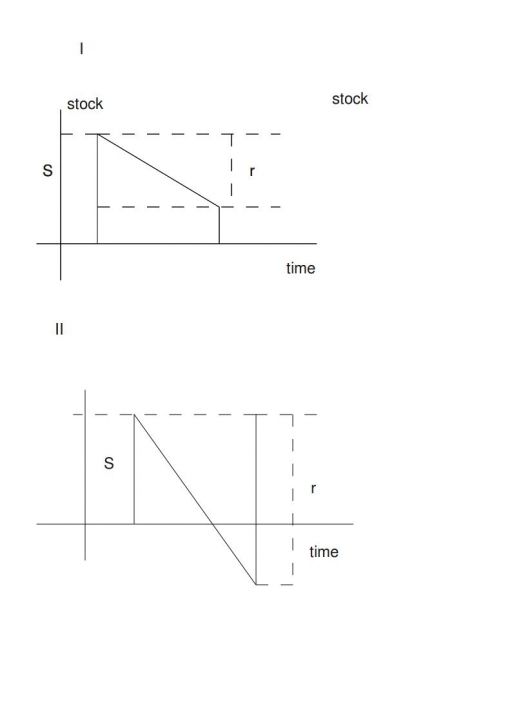
1) , i.e there is a positive remainder in the warehouse at
the end of the period. Storage cost is proportional to the area
under the stock graph.
Expectancy of this value is:
Therefore the average cost is:
2) . In this case the cost of both types is incurred. Again using the geometrical approach we find that cost elements are proportional to the areas of the triangles. The same argument as above gives the answer:
Thus the total cost is given by the following expression:
Marginal analysis is used to determine the optimal stock level. Optimal value of minimizing satisfies the relation:
(here my memory is abit vague, so I am giving it without proof and without guarantee)
Practically this means calculating for a series of the values of s until the above double inequality holds.