Further to the discussion of the cargo traffic through a port started in the previous post, i want to get together some thoughts and results obtained so far. What is missing here is only a leap into probabilistic formulas (i believe Poisson is just inevitable), but i'm still lacking confidence to assemble the whole thing in a working model.
Assume, we have cargo coming in at a daily rate of units, where n is the number of time period concerned (day in our case). Daily gate-out rate shall be units. Then daily stock can be found recursively:
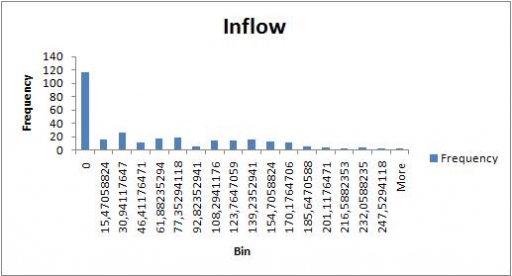
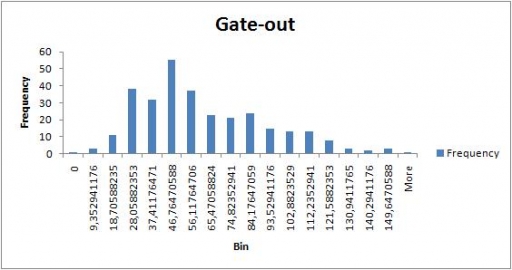
Mean storage time can be calculated as the total amount of warehouse work (see the previous post) divided by the total amount of cargo put through:
In a continuous case it should obviously look like this:
I took this definition form some old textbook and just made it complicated. However, it seems very natural and works perfectly in practice. It looks like formula for the center of gravity of the daily stok graph, but with changed order of summation (integration)
If calculations are made on a daily basis, the formula can be simplified as folows:
Note, that if at the start of calculations there is some initial stock with mean storage time per unit, the formula needs a small correction:
It is obvious that on the long run the effect of such correction is negligible (which is also proved by actual observations).
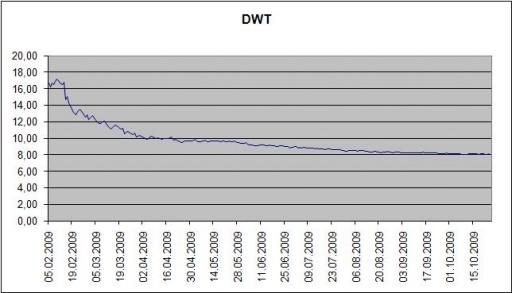
Applying the Little's formula to the above result we obtain the expression for the required warehouse space at every moment n: