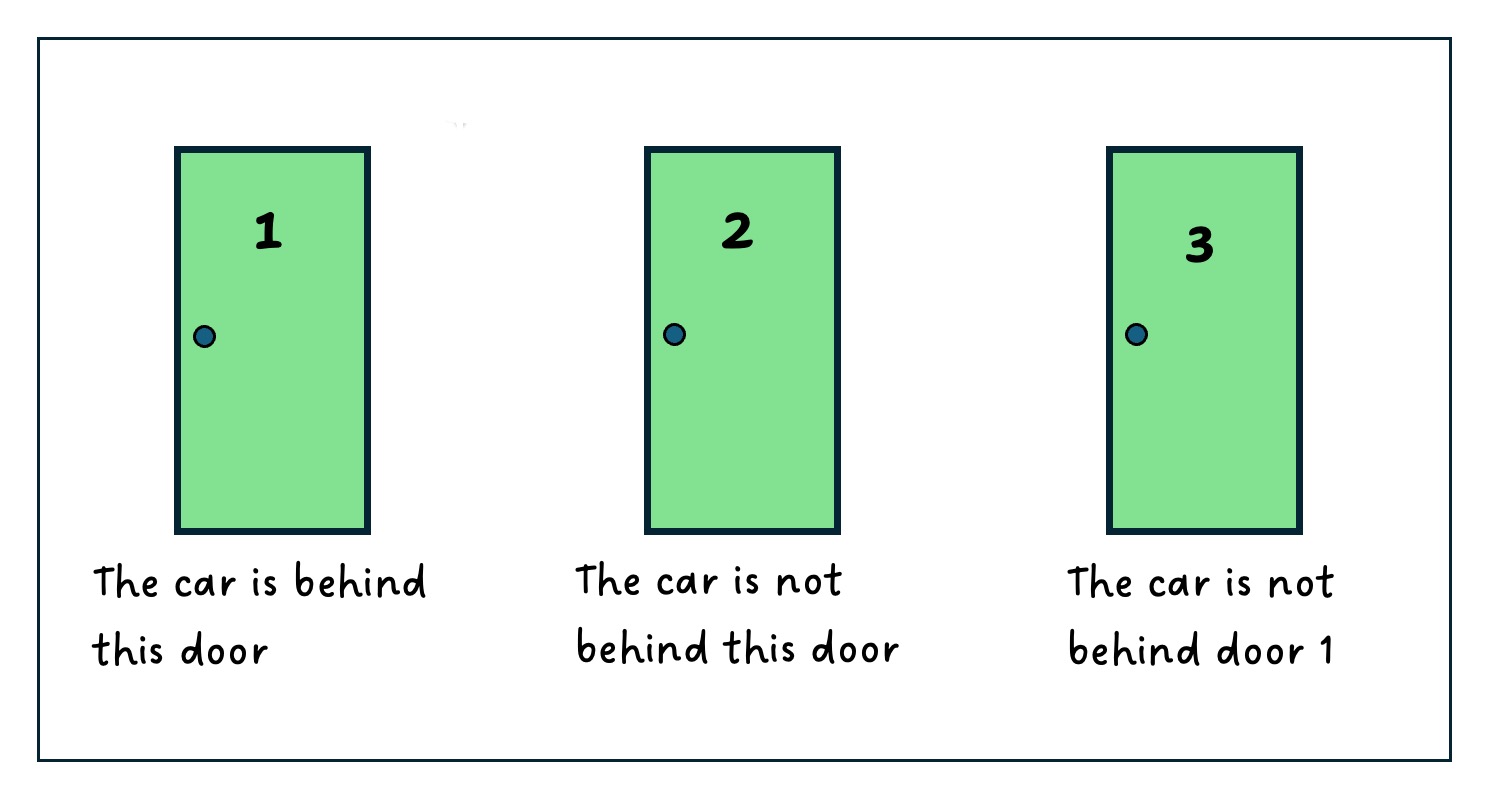
In this puzzle we are given three doors, one of which hides a car we can win if we are smart. Each door carries a statement and we are given that exactly one of these statements is true. So can we locate the car?
It's tempting to read the statements and start thinking 'If this true, what will follow?' or 'If this s false, what will follow?' and I can feel myself being tugged in that direction. But that usually isn't the best approach with puzzles like this. It's better to imagine putting the car behind each door in turn and see what that does for the truth or falsehood of each of the three statements.
So, suppose the car is behind door 1. Then statement 1 is true (the car is behind door 1) but so is statement 2 true (the car is not behind door 2). But this runs contrary to the fact that only one statement is true. So the car cannot be behind door 1.
Now let's skip to the last door and imagine it is the one that hides the car. Then statement 1 is false (the car is not behind door 1). Statement 2 is true (the car is not behind door 2), and statement 3 is also true (the car is not behind door 1). This again runs contrary to the fact that only one statement is true. So the car cannot be behind door 3.
That leaves door 2. If the car is behind door 2 statement 1 is false (the car is not behind door 1). What about statement 2? Well, that is also false, if the car is in fact behind door 2. And statement 3? Well it's true (the car is not behind door 1), and it's the only statement that is true. So this and only this fits the information we have been given, and the car must be behind door 2.
I think this puzzle has been skilfully crafted, because the car is behind a door that carries a false statement saying it's not behind that door, a neat twist!