Fig.1 A teenager on a quest for love
As a sixteen year old virgin the feelings I had for a girl had me indulging the sensations and plotting where it would go. It ended in tears - she took a fancy to my older brother. If anything happened, it was all in my head. She said I was in love with the idea of being in love. True. I wanted to record and reflect on all that I was going through, attempting to find a pattern in it. Any pattern, any model, is a crude simplification of reality. Learning above love or learning about learning as I've been doing these last four years is just as messy.
There's a dangerous interface between the academic and the popular, the scholarly paper and the journalist, where a plausible hypothesis passes for the truth. In the New York Times earlier last week a reporter interpreted the entry in a blog where the author suggests that learning isn't linear, but logarithmic. There's a ring of truth to it: achieving a grade, for example, above a certain figure (it differs by person, subject, module, stage in learning, proficiency and aptitude for the subject). There's also a ring of truth in the suggestion that some things are toughest at the beginning, while others are toughest at the end. The mistake is to think that such a model can be applied universally.
Any linearity is a model, an interpretation of reality, not reality itself. Several models I would refer to as alternatives to logarithmic and exponential, offered by this author and the NY Times journalist's misinterpretation would be:
Fig.2 In the flow
a) a straight diagonal line at 45 degrees with 'In the flow' as the title to illustrate the theory of getting 'in the flow' as a product of responding to stress on the one hand and learning or coaching to meet the challenge on the other as developed over decades by Miihaly Csikszentmihalyi
Fig. 3. The Forgetting Curve
b) the 'forgetting curve' developed over a century ago by Hermann Ebbinghaus
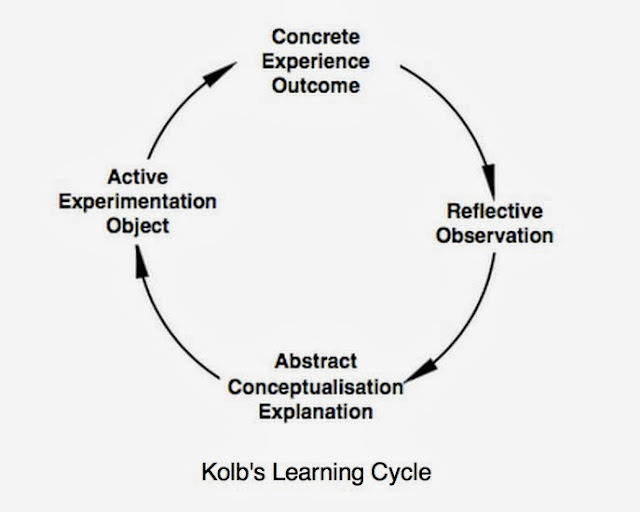
Fig.4. The Learning Cycle
c) the learning cycle, so a circle, developed by David Kolb.
Fig. 5 The learning thermal
d) My take on this is of an ascending spiral - which assumes constant progress. The reality is that we often hit turbulence, change or minds, come back to ground, gain a propeller, lose a leg ... Enough. I'll work this up when I can in a separate 'paper' and post in due course.
Oh heck. There are another two models I need to add to this:
Fig. 6 Activity Theory
e) Activity Theory, which is a triangle with six interconnected nodes (Yrjo Engestrom) and
Fig. 7. Network Theory
f) 'connectedness' (George Siemens claims credit) which is the 21st century take on an ever-present vision of how we learn ... which is related increasingly to 'network theory' which is complemented by current thinking on neuroscience - put crudely that all thoughts and ideas, their creation and memory are the product of the brain connecting at least seven now recognised clusters in different parts of the brain. Is 'network theory' the science behind the assumption of connectedness though?