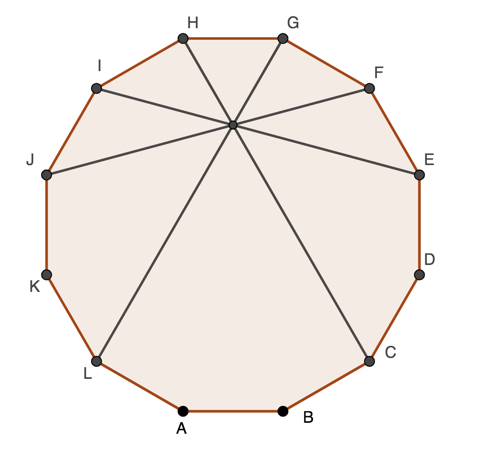
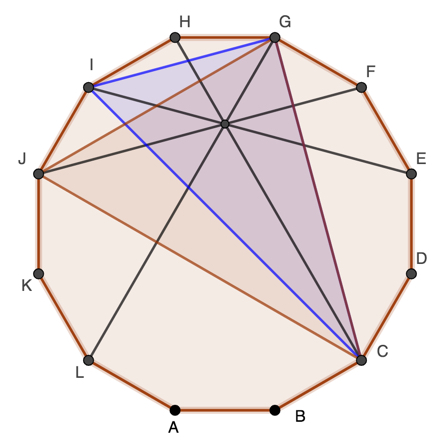
A few days ago I wrote about an elegant proof that a regular dodecahedrons has 4 diagonals that all intersect at a point other than the centre of the polygon, see https://learn1.open.ac.uk/mod/oublog/viewpost.php?post=248909
Since then I have found a paper by Poonen and Rubenstein [1] in which they completely solve the problem of concurrent diagonals in regular polygons. They prove several interesting facts, including:
If the number of sides is odd there can never be 3 concurrent diagonals.
The smallest number of sides that allow 3 diagonals to meet at a point other than the centre is eight, for diagonals twelve sides are needed, and for 5 concurrent diagonals eighteen sides.
To get more than 5 diagonals meeting at a point other than the centre we need to go to thirty sides. The regular triacontagon has sets of 6 and 7 concurrent diagonals.
And then suprisingly it stops. No regular polygon, however many sides it has, can have eight or more diagonals intersecting at a point other than the centre.
[1] https://mathproblems123.files.wordpress.com/2011/03/ngon.pdf