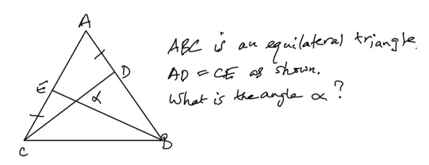
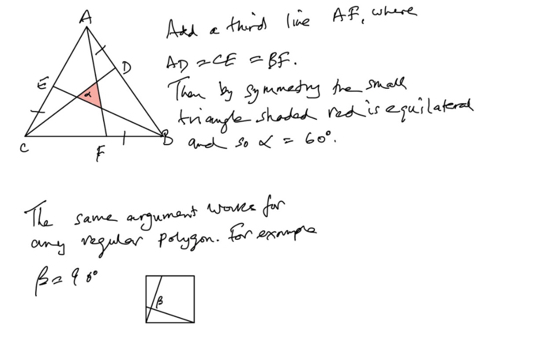
Following my earlier post about CHECKBOOK, I wrote a Python program to find dictionary words with the property they have symmetry about a horizontal mirror line; if you invert them, they remains the same. I used the UK Advanced Cryptics Dictionary, by Ross Beresford (240732 words) as my word source.
Here is the full list of then 352 results. As you might expect some of the words are a wee bit obscure.
['B', 'BE', 'BECK', 'BECKED', 'BED', 'BEDDED', 'BEDE', 'BEDECK', 'BEDECKED', 'BEDIDE', 'BEE', 'BEEB', 'BEECH', 'BI', 'BIB', 'BIBBED', 'BIBCOCK', 'BICE', 'BICKIE', 'BID', 'BIDE', 'BIDED', 'BIKE', 'BIKED', 'BIKIE', 'BIO', 'BIOCIDE', 'BO', 'BOB', 'BOBBED', 'BOBBIE', 'BOCCE', 'BOCHE', 'BOCK', 'BOCKED', 'BOD', 'BODE', 'BODED', 'BODICE', 'BODIED', 'BOH', 'BOK', 'BOKE', 'BOKED', 'BOKO', 'BOO', 'BOOB', 'BOOBED', 'BOOBOO', 'BOOBOOK', 'BOODIE', 'BOODIED', 'BOOED', 'BOOH', 'BOOHED', 'BOOHOO', 'BOOHOOED', 'BOOK', 'BOOKED', 'BOOKIE', 'BOX', 'BOXED', 'C', 'CEDE', 'CEDED', 'CEDI', 'CEE', 'CH', 'CHE', 'CHECK', 'CHECKBOOK', 'CHECKED', 'CHEEK', 'CHEEKED', 'CHI', 'CHIC', 'CHICH', 'CHICHI', 'CHICK', 'CHICO', 'CHID', 'CHIDE', 'CHIDED', 'CHIK', 'CHOC', 'CHOCHO', 'CHOCK', 'CHOCKED', 'CHOCKO', 'CHOCO', 'CHOICE', 'CHOKE', 'CHOKED', 'CHOKO', 'CHOOK', 'CHOOKIE', 'CID', 'COB', 'COBB', 'COBBED', 'COCCI', 'COCCID', 'COCCO', 'COCCOID', 'COCK', 'COCKED', 'COCO', 'COD', 'CODDED', 'CODE', 'CODEBOOK', 'CODED', 'CODEX', 'COED', 'COHO', 'COHOE', 'COKE', 'COKED', 'COO', 'COOED', 'COOEE', 'COOEED', 'COOK', 'COOKED', 'COOKIE', 'COX', 'COXED', 'D', 'DEB', 'DEBBIE', 'DECCIE', 'DECIDE', 'DECIDED', 'DECK', 'DECKED', 'DECKO', 'DECKOED', 'DECO', 'DECODE', 'DECODED', 'DECOKE', 'DECOKED', 'DEE', 'DEED', 'DEEDED', 'DEEK', 'DEICIDE', 'DEID', 'DEKKO', 'DEKKOED', 'DEO', 'DHOBI', 'DI', 'DIB', 'DIBBED', 'DICE', 'DICED', 'DICH', 'DICK', 'DICKIE', 'DID', 'DIDICOI', 'DIDO', 'DIE', 'DIEB', 'DIED', 'DIKE', 'DIKED', 'DIODE', 'DIOXIDE', 'DIXI', 'DIXIE', 'DO', 'DOB', 'DOBBED', 'DOBBIE', 'DOBCHICK', 'DOC', 'DOCK', 'DOCKED', 'DOD', 'DODDED', 'DODO', 'DOE', 'DOEK', 'DOH', 'DOO', 'DOOB', 'DOOK', 'DOOKED', 'E', 'EBB', 'EBBED', 'ECCE', 'ECCO', 'ECHE', 'ECHO', 'ECHOED', 'ECHOIC', 'ECO', 'ECOCIDE', 'ECOD', 'ED', 'EDDIC', 'EDDIE', 'EDDIED', 'EDDO', 'EDH', 'EE', 'EEK', 'EH', 'EHED', 'EKE', 'EKED', 'EO', 'EX', 'EXCEED', 'EXCEEDED', 'EXCIDE', 'EXCIDED', 'EXE', 'EXODE', 'EXODIC', 'H', 'HE', 'HEBE', 'HECH', 'HECK', 'HEED', 'HEEDED', 'HEID', 'HEIDE', 'HEX', 'HEXED', 'HI', 'HIC', 'HICK', 'HICKOK', 'HID', 'HIDE', 'HIDED', 'HIE', 'HIED', 'HIKE', 'HIKED', 'HO', 'HOB', 'HOBO', 'HOBOED', 'HOC', 'HOCK', 'HOCKED', 'HOD', 'HOE', 'HOED', 'HOH', 'HOI', 'HOICK', 'HOICKED', 'HOIK', 'HOIKED', 'HOKE', 'HOKED', 'HOKI', 'HOO', 'HOOCH', 'HOOD', 'HOODED', 'HOODIE', 'HOODOO', 'HOODOOED', 'HOOK', 'HOOKE', 'HOOKED', 'HOX', 'I', 'IBEX', 'IBO', 'ICE', 'ICEBOX', 'ICED', 'ICH', 'ID', 'IDE', 'IDO', 'IKE', 'IO', 'IODIC', 'IODIDE', 'K', 'KEBBIE', 'KEBBOCK', 'KEBOB', 'KECK', 'KECKED', 'KED', 'KEECH', 'KEEK', 'KEEKED', 'KEX', 'KHOIKHOI', 'KIBE', 'KICK', 'KICKED', 'KID', 'KIDD', 'KIDDED', 'KIDDIE', 'KIDDIED', 'KIDDO', 'KIKE', 'KIKOI', 'KO', 'KOB', 'KOBE', 'KOI', 'KOODOO', 'KOOK', 'KOOKED', 'KOOKIE', 'O', 'OB', 'OBECHE', 'OBI', 'OBIED', 'OBO', 'OBOE', 'OCH', 'OCHE', 'OD', 'ODD', 'ODE', 'ODIC', 'OE', 'OH', 'OHIO', 'OHO', 'OI', 'OIK', 'OK', 'OKE', 'OKED', 'OO', 'OOH', 'OOHED', 'O', 'OX', 'OXHIDE', 'OXIDE', 'X', 'XEBEC', 'XI']