Woodworm. That's a boring life.
Personal Blogs
Knock-Knock!
Who's there?
Iris.
Iris who?
Iris you in the name of the law!
I was watching a very interesting lecture on YouTube, From Ronald Ross to ChatGPT: the birth and strange life of the random walk, and the speaker said "WQ" was one of the few letter pairs that do not appear in English words, and then went on to suggest we could neologise a word "cowquake" and imagine a thunder of hooves.
Well, this was a challenge, surely "WQ" must exist in some real words. So of course I went to look for them.
1. Does "cowquake" exist? (You might argue it does now, even if it didn't before).
2. Are there any other words containing "WQ"?
This is what I found on initial investigation.
1. The OED has "cow-quakes", a name for quaking grass, but I guess the hyphen disqualifies it.
However I found a BBC reference to "cowquaker", an 'off the scale thunderstorm' that frightens the cows. So looks like cowquaker exists, even if cowquake is debateable. Still I couldn't find the word in the OED.
2. Googling for words with "WQ" in throws up many acronyms and company names, and the Cornish town Newquay, plus the odd unusual word in other languages. But these don't really count, and the only promising candidates I'd found by this point are "crowquill" and "snowquake".
A crowquill is a quill pen made not from a goose feather but with a feather from a crow, and the name is now used for a fine-tipped metal nib for map drawing and similar work. The OED hyphenates the word though, and Merriam-Webster makes two words of it, so this is another disputable example.
As for "snowquake" neither the OED nor Merriam-Webster recognise it, although I did find an Urban Dictionary entry:
When its snowing/snow blanketing the ground and you have an earthquake at the same time.
At this point in my search, the only reliable examples seemed to be "cowquaker" and "crowquill", and the neither are indisputably a single word.
But luckily MW has a useful similar words feature, and this threw up "cawquaw", the Canadian porcupine, from the Cree word for the animal. And bingo, the OED has this!
cawquaw, n.
The North American porcupine, Erethizon dorsatus (family Erethizontidae), which has blackish-brown fur and dark quills with white tips.
It wasn't always spelt exactly the same, but the OED give a citation from 1840 which seems to establish the modern spelling
Penny Cyclopaedia vol. XVIII. 415/2
I think this is a bona fide single word with "WQ" in it, even if it is (as the OED puts it) now rare, and my search has been successful.
But are there other examples/ If you find any please put them in the comments!
A montage of street art photos someone sent me from Lagos in Portugal. The one with the junction box commemorates the Carnation Revolution of 1974.

This is our new planter and some really gorgeous flowers.

"I see you've got a new set of choppers", said Tom accidentally.
P.S. I made that one up, but here is a related TS from an article at Merriam-Webster
“I’ve dropped the toothpaste”, said Tom crestfallenly.
Although the Ancient Greek mathematicians discovered an enormous amount about geometry, in modern times a number of rather nice facts have been found that the Greeks didn't know about. One of these is Bottema's Theorem, named for Oene Bottema, a Dutch mathematician of the 20th century. It goes like this
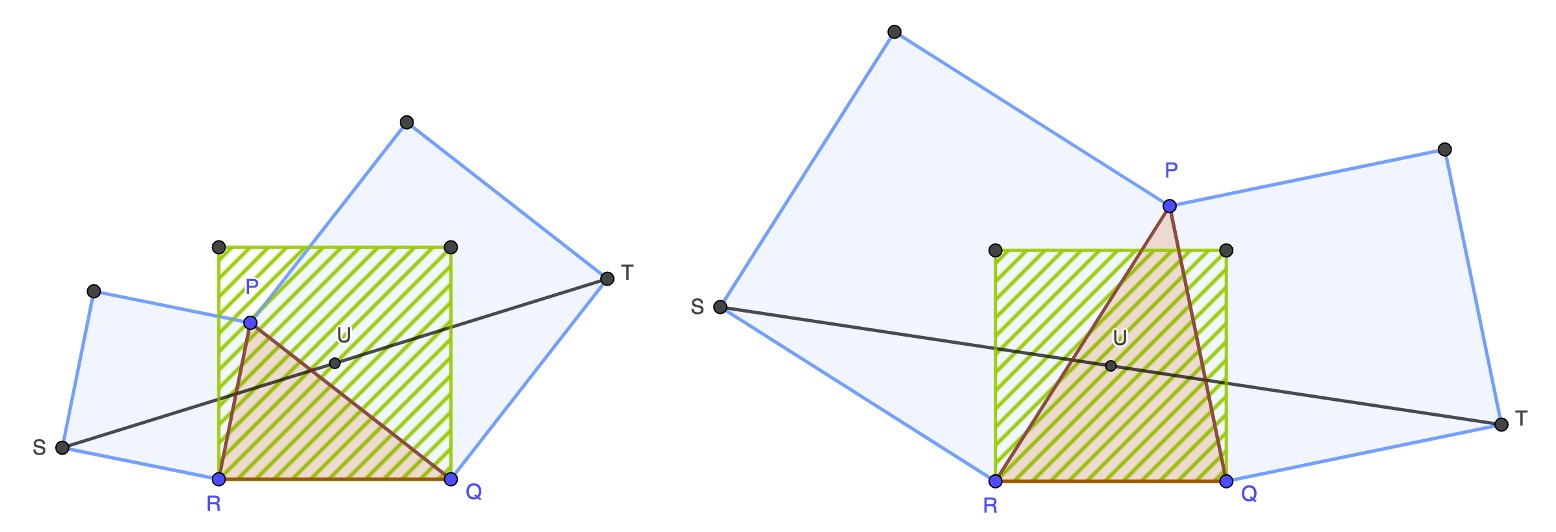
Suppose we have a triangle, PQR in the diagrams, and draw squares on two of its sides as shown. Draw a line joining the two vertices of the square that lie opposite to the vertex P and mark the midpoint U of the line that joins them.
Then the midpoint lies at the centre of a square resting on the base of the triangle and rather unexpectedly this is true wherever we move move the vertex P. The diagrams above show two positions of P and you can see that the position of U is indeed the same in both cases.
There are quite a few websites that discuss the theorem and give proofs, and there are also some nice animations and YouTube videos that demonstrate the fact that the midpoint is independent of P's position.
There are also some published variations on Bottema's theorem, but here is a neat one one I discovered by chance and which I haven't seen anywhere and which is new, to me at least.
Bottema's theorem works not just for squares but for any regular polygon with an even number of sides. For example, here is an example where the polygons have six sides.
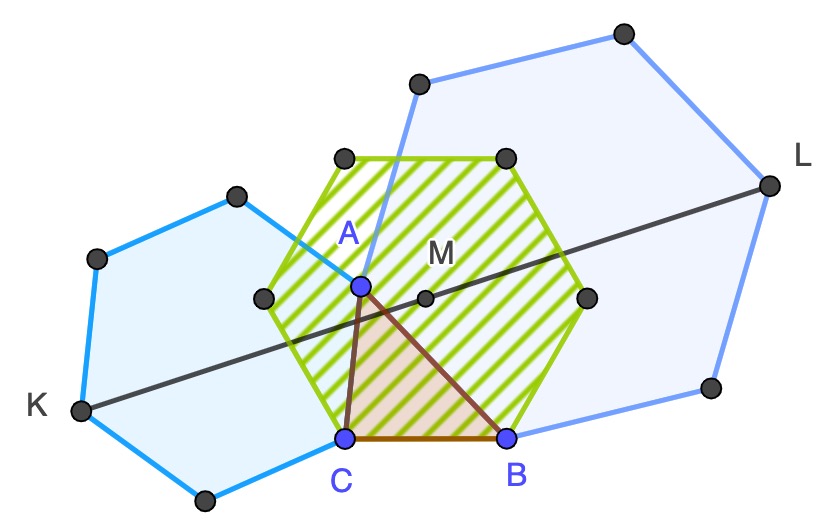
Notice that the midpoint M is now the centre of a third hexagon, rather than a square, resting on the bases of the square, and as with the square case the position of the midpoint does not depend on the position of vertex A.
If we instead erect octagons on the sides of the triangle then the midpoint will again be independent of the location of A, and will be the centre of an octagon resting on the base of the triangle. We can construct analogous configurations for any even number of sides, and the midpoint will always be fixed in the same way. I think that's rather neat and I was pleased when I discovered it.
It's often described as the temple of Diana it seems, but this is not attested and current thinking is it was dedicated to the Emperor Augustus, who was declared a god after his death in 14 CE.
The temple was knocked about by the Visigoths in the 5th century. In the Middle Ages it became part of the city's castle, and then in modern times it was gradually restored to what we can see today.
Évora is a very interesting name etymologically; ebora meant "(place) of trees" or perhaps "(place) of yew trees" in the language of the pre-Roman Celts and has survived with little change to the present day.
The same root is the origin in the city name of York, although it has been modified much more. You can read about its long winding journey on Wikipedia and elsewhere, but here's the story.
The Romans Latinised Ebor or Ebora to Eboracum, which the incoming Angle and/or Saxons thought was Eoforwīc, from Old English eofor = wild boar and wic = village (an element found at the end of dozens of modern English place names, typically as -wich).
But later Vikings established a colony there, and changed the name to Old Norse Jorvik, the first element of which is recognisably the same as – cognate with – eofor, followed by -vik, which meant something like "inlet". So by now we have got from Yew Grove to Wild Boar Cove. Eventually of course this was shortened to modern-day York, and there you have it.
“If I asked ever so nicely, could I have that sofa and chairs?”, asked Tom sweetly.

The Olympian Gods and Goddesses on Mount Olympus lived on ambrosia. I've never thought much about what ambrosia was, I just assumed it was some delicious food reserved for deities and denied to mortals, and probably so delightful that the gods could put up with eating it day after day ("Oooh goody, ambrosia again, my favourite.")
However I just found out this diet is what made the gods immortal.
I'm currently reading the wonderful book Words from Hell by the witty and erudite Jess Zafarris, who blogs, writes and makes podcasts about etymology. Reading the origins of the word murder, I was astonished to find the word ambrosia shares a common origin with murder. Whatever is the connection between these two things?
It turns out they are both descended from a root that was something like mer-, which means rub out or harm or die and which appears in many words like mortal and mortuary and so on. It pops up in ancient Greek as ἄμβροτος, ambrotos. The a- means not and mbrotos meant mortal, so the word ambrosia literally meant "not-mortal".
The Greek gods also had a special drink, nectar. This seems to mean essentially the same thing; the Ancient (and modern) Greek νεκροs, necros, means dead or death, and the -tar element is from a root tere which has the sense of through or crossing or overcoming. So nectar helped the gods overcome death and was the perfect drink to have with your ambrosia.
At least if you were an Olympian deity you didn't have to worry about what to have for lunch. This reminds me of an anecdote about the physicist Richard Feynman, who wrote about the problem of choice and said "... when I was a student at MIT. I got sick and tired of having to decide what kind of dessert I was going to have at the restaurant, so I decided it would always be chocolate ice cream, and never worried about it again."
Speaking of rain I saw this rainbow this other day. Although rainbows are a familiar sight, when one appeared all the people around me were quite excited, and I was too.

This got me wondering what rainbows are called in other languages. Is the name a compound, similar to the English rain+bow? On a quick look I found some where it was, and one or two rather different.
German is regen-bogen, evidently cognate with the English. Old English had regnboga, also very close, but it also had scurboga, and recalling that "sc" in Old English was pronounced as "sh" this would be shower-bow, which rather sadly is now lost. I think we shyould bring it back.
In French we have arc-en-ciel, "arc in the sky", so no reference to rain. Italian is arco baleno, which I think means something like "arc-flash", so that's a bit different, but still has the bow theme.
Latin was iris, borrowed from Ancient Greek I think. Iris was personification of the rainbows. Her name may have originally been Wiris, starting with the archaic digamma, a letter lost in later Greek.
Modern Greek has a different word from Ancient Greek and it baffled me at first, ourano toxo. But after some head-scratching I recalled that Uranus was the personification of the sky and toxo means bow (as in toxophilite, one who likes archery, and the word archer must also be related to arcs/bows). So the Greek expresses the same idea as the French arc-en-ciel.
The last one I looked at was Welsh, which has enfys. The etymology of this is trickier. The en- bit could be an "intensifier", a prefix that adds some kind of emphasis to the following element, and the fys part could be connected to finger or ring, so the origin might have been something like great ring.
“That egg isn’t going anywhere”, said Tom ecstatically.
I don't know what the weather is like where you are but where I am it's
Raining. Again.
I thought of the nursery rhyme
"Rain, rain, go away/Come again another day",
and that set me wondering if there is a similar children's verse in other languages.
When I tried French, I stumbled across the wonderful Mots D'Heures: Gousses, Rames, by Luis d'Antin van Rooten, which the author claims were verses "From the d'Antin Manuscript, Discovered, Edited and Annotated". [1][2]
Here's Verse 16. Try reading it aloud in your best French accent
gueux éveille.
Gomme à gaine,
en horreur, taie."
Van Rooten provides scholarly note to help us with the archaic language of the verses, for example Verse 16 he explains as
"Queen, Queen, arouse the rabble
Who use their girdles, horrors, as pillow slips."
Here are a couple more titles from the book - can you work them out?
Et qui rit des curés d'Oc?
Lit-elle messe, moffette
[1] Wikipedia

“My cuddly bear is luminous”, Tom gloated.
This astonishing tiling with 7-fold symmetry is build from identical pentagonal tiles.
I find the way it is constructed fascinating.
The drawing is by Tom Ruen and I think the discoverer of the pattern was Klaassen, who showed in 2016 that a similar pentagonal tiling can be found for any degree of symmetry, see here.
“I’m here”, said Tom presently.
St Neot, d. 877, was was a monk from Glastonbury Abbey who moved to Cornwall to be more isolated (the word monk is from Greek μονος monos = alone). His piety and devotion made him famous and a number of miracle were connected with him. He visited the Pope, and on the latter's bidding found a monastery in Cornwall, where his remains were kept after his death. The relics attracted many pilgrims and an associated flow of income. Here is a rather impressive stained glass window from the church in St Neot's in Cornwall.
About a hundred years on a different monastery was founded in Cambridgeshire, at what was then called Eynesbury (probably after an earlier saint who may have existed called Arnulf) but is now named St Neot's.
Monks from this second abbey seem to have though St Neot's remains would be a useful pull for pilgrims, so they travelled to Cornwall and the saint's remains were (as Wikipedia delicately puts it) "abstracted from Cornwall without permission, and lodged at Eynesbury". In other words monks from Cambridgeshire went to Cornwall, snatched the bones and brought them back home.
Sure enough these relics brought a stead stream of visitors and a healthy revenue flow, but stealing these bones has always seemed to me a rather discreditable and cynical act, and I've often wondered too why the Cornish monks never staged a counter raid. Who knows?
Varignon's Theorom says that if we take any quadrilateral whatsoever and join the midpoints of its sides we (rather surprisingly) always get a parallelogram
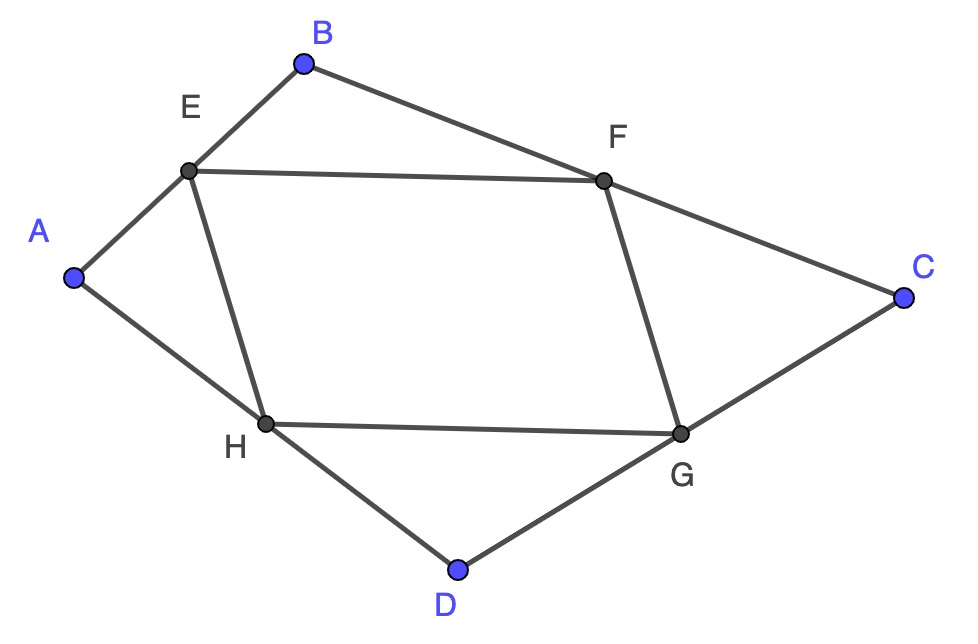
I give a neat and I hope fairly intuitive proof here.
Today I read about an elegant generalisation of this theorem. The page I've linked to has much more that this, but in my diagram below, which I drew using Geogebra, I've just illustrated the first case.
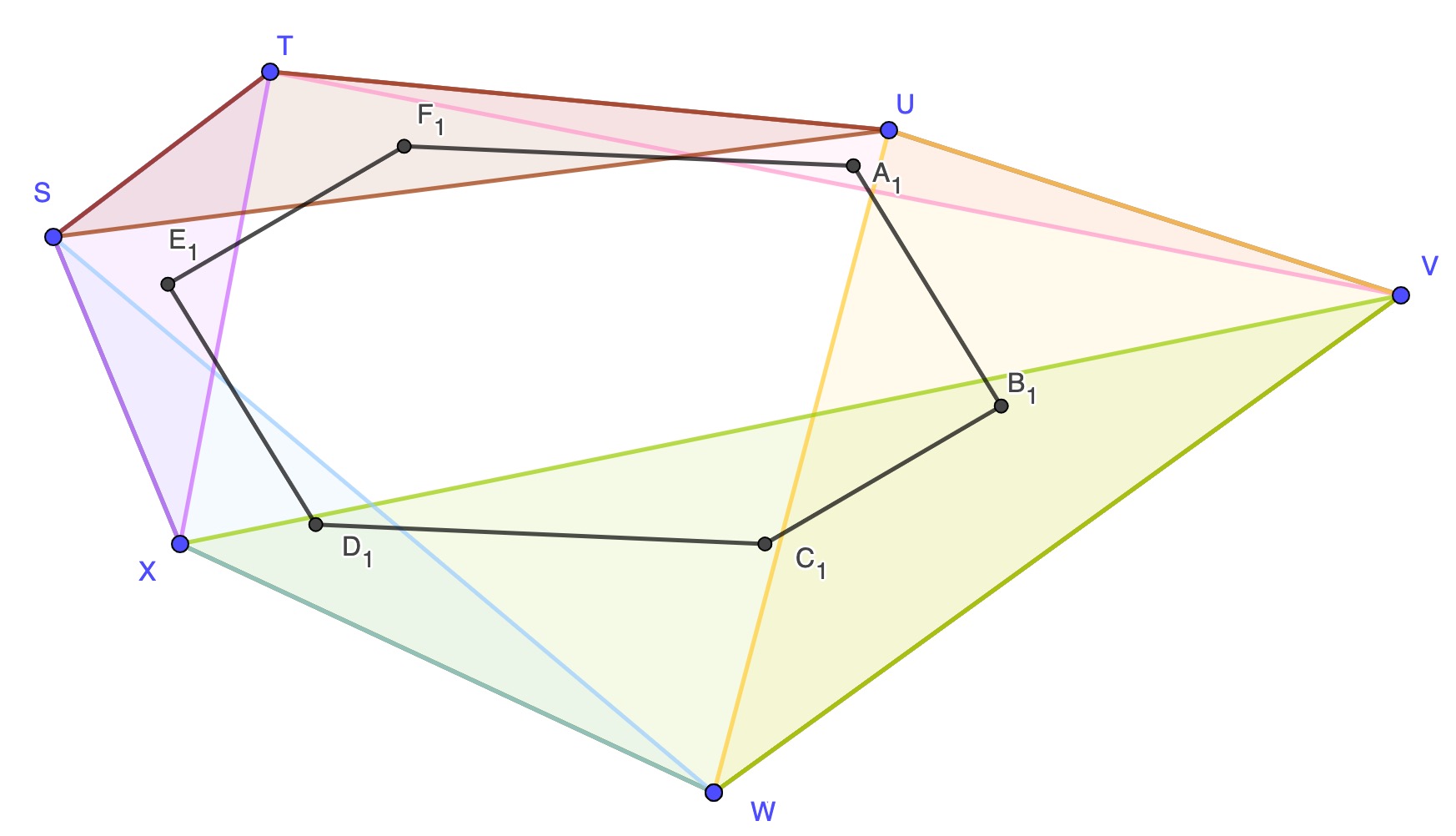
For any hexagon, STUVWX in the figure, form a triangle from each group of three adjacent vertices in turn. Mark the centroid, i.e. the centre of gravity, of each triangle, and join them up to form a hexagon A1B1C1D1E1F1 as shown.The each pair of opposite sides of the new hexagon are parallel and of equal length, in other words the new hexagon is analogous to a parallelogram, but with six sides rather than four.
"I seem to be developing tooth decay", said Tom precariously.
Today I picked up a local saying I'd not heard before:
"He's ninety-twelve years old".
Meaning he's very old. I like it, it's vivid and humorous.
I always thought of "Earthling" as a fairly modern sci-fi type of word but I've learned from the excellent "Words Unravelled" podcast and YouTube channel that it was already word in Old English. It meant a ploughman and was still used in that sense until the early 1800s. From about 1600 it came to have the modern sense of someone who lives on the Earth.
It's interesting because it uses the suffix -ling, which has several loosely related meanings. Originally in OE it (usually) implied a person concerned with or related to some particular thing (hence earthling) and we also have hireling (someone hired) and sibling (originally a kinsman, now just a brother or sister of course, and I used to think it was just a modern word, but not so). Starling the bird also seems to use the same construction, and birds crop again below
Nowadays it can just be a diminutive, as in gosling, duckling, sapling or nestling, but can sometimes also have dismissive connotations, the OED gives the examples godling, lordling, kingling, princeling. A princeling is definitely some way down the scale of princeliness (yes it really exists).
Chat GPT threw up quite a few more: weakling, fledgeling, hatchling, seedling, underling, yearling, changeling, foundling, stripling, mostly implying some sort of smallness or weakness.
"I love camping", said Tom intensely.
Sun Dogs are caused by the light from the Sun being refracted by ice crystals. My brother snapped this one a couple of days ago, on the 21st of June.

They appear 22 degrees horizontally from the Sun and if you are lucky one on each side of the Sun, depending where the ice crystals are, although it's commoner to only see one.
What’s the most difficult tongue twister? It’s hard to say.
This blog might contain posts that are only visible to logged-in users, or where only logged-in users can comment. If you have an account on the system, please log in for full access.