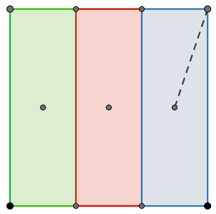
This puzzle concerned three park rangers who are responsible for overseeing a park in the shape of a square of side 100 km. The puzzle is to partition the park between the rangers so each is responsible for the same area, and to station them so the greatest distance any ranger may need to travel to reach a point in their allocated regions is less than it would be with the simple approach of dividing the park into three identical rectangular strips as shown below..
This problem was posed in the November 1952 edition of the American Mathematical Monthly [1] and a solution provided that also met the further condition that each point in the park be allocated to the ranger stationed nearest to it. The solution given is below.
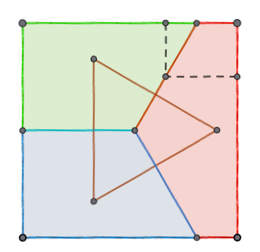
The oblique lines pass through points side/3 and side/4 from the edges of the square, as indicated by the dotted segments, and are at 120° to one another. One ranger station is at the intersection of two long diagonals of the pentagon at right, and the other two are found by reflecting this point in the boundary lines. The three ranger stations are then at the vertices of an equilateral triangle.
This satisfies all three requirements: equal area, reduced maximum travel distance compared with the three rectangle solution, and allocation of every point to the geographically nearest station.
However if we relax the last condition I think it is possible to reduce the maximum travel still further. Can you see how this could be done?
[1] Ogilvy, C. S., & Bankoff, L. (1952). E1001. The American Mathematical Monthly, 59(9), 634–635. https://doi.org/10.2307/2306773