It is possible to dissect an equilateral into 2, 3, 4 and 6 congruent parts, as seen in the sketches below.
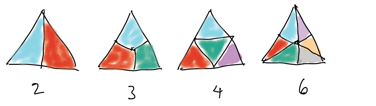
But what about 5 parts? This seems more tricky, if only because it is hard to find a 5-fold symmetry associated with an equilateral triangle, and although I don't know of a proof, I think it is probably impossible - at least if we demand that each piece be a connected shape.
However, if we sacrifice this requirement and allow detached parts, a "quinquisection" then becomes possible. Here is a highly ingenious solution found by Mikhail A. Patrakeev, whose paper can be found here.
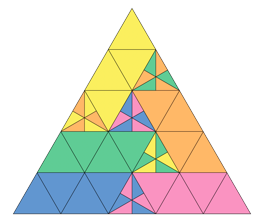
This remarkable construction uses a sort of hybrid symmetry, exploiting three fundamental isometries (transformations that preserve lengths and angles): reflection, translation and rotation.
Firstly Pink and Blue are congruent because they are refections of one another in the line down the middle of the triangle. So they are congruent.
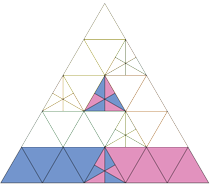
Secondly, Green is a translation of Blue, a shift up and right at an angle of 60 degrees. So Green is congruent to Blue (and hence to Pink).
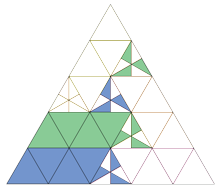
Lastly, Yellow and Orange are rotations of Green by 120 and 240 degrees, so they are congruent to it and hence to Blue and Pink as well.
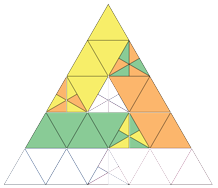
And therefore all five sets are congruent as claimed. A very pretty and clever solution.