There is a class of geometric problems that ask about covering shapes with other shapes. Some have practical applications but mainly they are studied for interest, and because they can be easy to state but unexpectedly hard to solve.
One type of problems concerns covering a circle with 1 x 1 squares. If we use 1, 2, 3... squares, what is the biggest circle we can completely cover in each case?
Here are the optiomal arrangements for 1, 2, and 3 squares
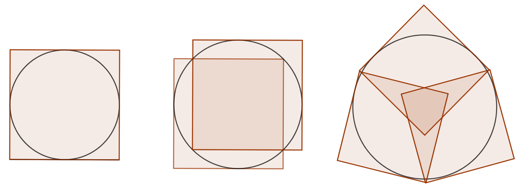
I constructed the first two in GeoGebra but the third is a sketch based on a diagram by Erich Friedman.
These have been proved to be optimal. Here are even sketchier pictures of the other two cases where the best possible arrangement is known with certainty.
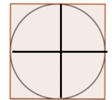
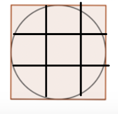
You may see a pattern here, something like "when the number of square is a square number 12 =1, 22 = 4, 32 = 9 etc, the best arrangement is just a square grid. Obvious really.
But it's not true! When we get to 16 the pattern breaks down and the surprising arrangement below turns out better. I didn't say best, because this is just the best known, and it might be possible to improve on it. By this point I'd so many diagrams I decided to cheat and simply copy Eric's amazing diagram.
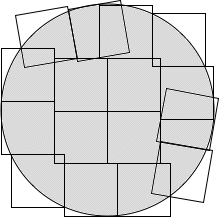
Kind of crazy but it does have a line of symmetry. Erich Friedman's github page here gives best known solutions up to 18 squares and they are all symmetrical about a line, but this not a given; there may be improved solutions with now symmetry, it's perfectly possible.
Here's a puzzle to end with; if we go back to the case of two squares, whar is the radius of the circle? You can look it up on Erich's page of course, but can you work it out?