Sangaku were geometrical puzzles from the 18th, 19th and early 20th centuries, painted on wooded tablets and hung in Japanese temples. Here is a problem I came across which is either a Sangaku or inspired by that tradition. It is very simple to state.
Inside a circle another smaller circle is drawn which is tangent to the bigger circle and to a diameter of the bigger circle.
An even smaller circle is then drawn which is tangent to the diameter and to both the other circles, as shown in Figure 1.
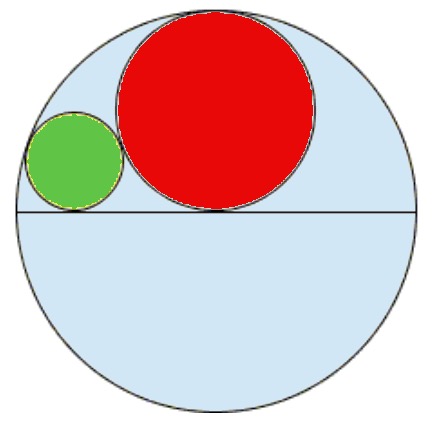
Figure 1. The green circle is tangent to the red circle, the diameter and the enclosing blue circle.
- What is the radius of the smallest circle, as a fraction of the radius of the biggest circle?
- Can you see how to construct the smallest circle using straightedge (i.e. a ruler with no makings on it) and compasses? If you can it should help you answer the first question.
I had a lot of fun solving this problem which turns out to have a really nice answer. I'll post my solution, which I am pretty comfident is correct, at the end of the week.