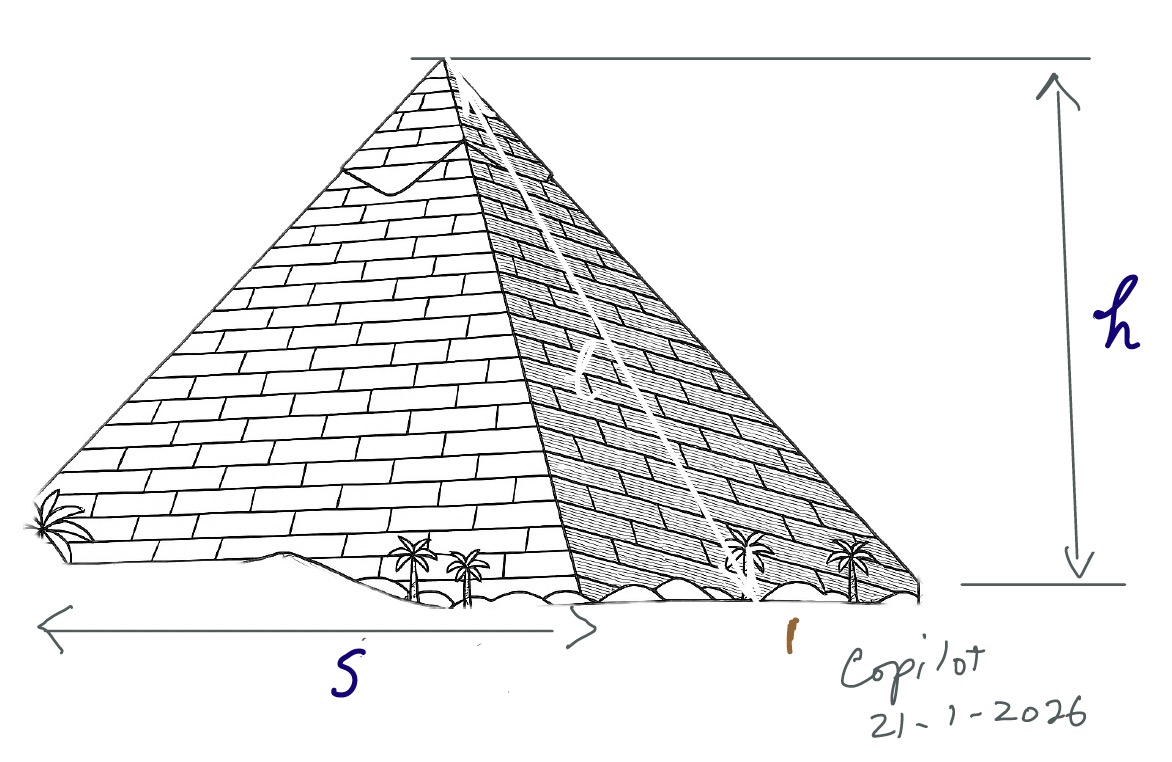
I asked here what ratio between the height of a pyramid and the length of its sides would give the greatest volume for a given surface area. Below I will give two solutions, the first I think quite insightful and intuitive, and doesn't need much maths at all, but you have to take a particular fact on trust. The second is more fully worked out but does need some maths.
As well as the side length and height I've added the slant height to the sketch, because we shall use it later, and because it is often referred to in discussion about the proportions of pyramids. The Great Pyramid of Giza originally stood about 147 m tall and its side length at the base was about 230 m. If we work out the slant height and compute its ratio to half the base length it comes to about 1.623, which is sometimes said to be strikingly close to the Golden Ration.
And now: the solution to the puzzle. The height should be <drum roll>
times the side length. It's worth noting that this makes the slant height to half side length ratio , so Pharaoh's new pyramid will be a bit pointier than that at Giza with its ratio of 1.623.
Explanation 1 (intuitive)
Imagine the pyramid is just the top half of a solid whose other half is an inverted copy of the pyramid. What would it look like? Well, it would have eight faces and it's not hard to see it would be an octahedron.
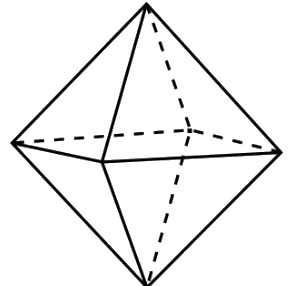
If you like you an imagine the bottom half being buried in the sand!
Our goal is to maximise the volume for a given surface and the octahedron that does that is the regular octahedron. It's also not too difficult to workout that if the octahedrons sides have a length of its height will be the diameter of a square of side length , which is and the height of the top half one half of that, which is .
This is a very pleasing explanation which feels intuitively correct but of course I have just claimed that the regular octagon is optimal without proof. However I'm not going to attempt a proof here, because I think making it watertight would be quite lengthy. If I can find or come up with a nice simple proof I'll write about it a separate post.
Explanation 2 (mathy)
Let the combined area of the four faces be , the slant height , the vertical height , as shown. Let the volume of the pyramid be .
Then firstly, using the formula for the area of a triangle and Pythagoras gives and respectively.
To avoid square roots later we square the first equation so we have . By substituting for and making the subject we obtain
Next the formula for the volume of a pyramid tells us that and it is convenien to square this also, giving . Substituting the expression for found earlier we obtain
We want to maximise rather the but they will both be maximised at the same value of . So we differentiate this expression and find the non-zero root. The derivative is
which is zero when . Plugging this into our expression for and tidying up we get .
Finally we get and that is the ratio of the optimal height to the side length.
PS This has bee a great project to practice my LaTeX!
Picture credit for octahedron: Wikimedia https://commons.wikimedia.org/wiki/File:Octahedron-MKL4.png