Algorithms 2 implemented a very simple
algorithm as a program. Despite its simplicity it still relied on two built-in
functions to get user input and display output. In all but the most trivial of programs,
modularity in the form of functions, objects, classes, components, modules and
packages is used to reduce the unassailable complexity that would otherwise arise.
Regardless of complexity, an algorithm
will often have applicability extending beyond a particular program and it is
generally useful to separate this functionality from program specific code by
factoring it off to a separate function. This article takes a look at functions
and some other basics, both in general and as implemented by Python.
You may be already acquainted with
functions to a greater or lesser extent. A function is a relation that maps an element from a set
of inputs to exactly one element in a set of outputs. A relation
is defined by input to output mappings: the same input always produces the same
output. Two or more inputs can produce the same output or every input can map
to a different output. The relation's inner workings, when they extend beyond
simple mapping, need not be known. They do not form part of its specification
and quite possibly there may be several different algorithms that implement the
same relation.
Exactly one output is crucial for a
function. Functions often use other functions and we cannot make use a function
that returns one output for a particular set of inputs, two for another and
fails to deliver at all for a third. The meaning of this single output
restriction will be discussed in greater detail later in the next article.
The parts of a function
An application program,
application or app. (called this to distinguish application software from
system software - the operating system for example) can generally be identified
by its performing some task or tasks for users or another application program.
It is a top level unit of modularity providing an interface to
its users that exposes functionality and hides inner workings, its implementation.
Functions exist at the other end of the scale but still present an interface hiding
details of the function's implementation.
Consider a function that accepts two
numbers, total and number with a string representing an operator. It applies number to total using the operator
corresponding to the string and returns the result:
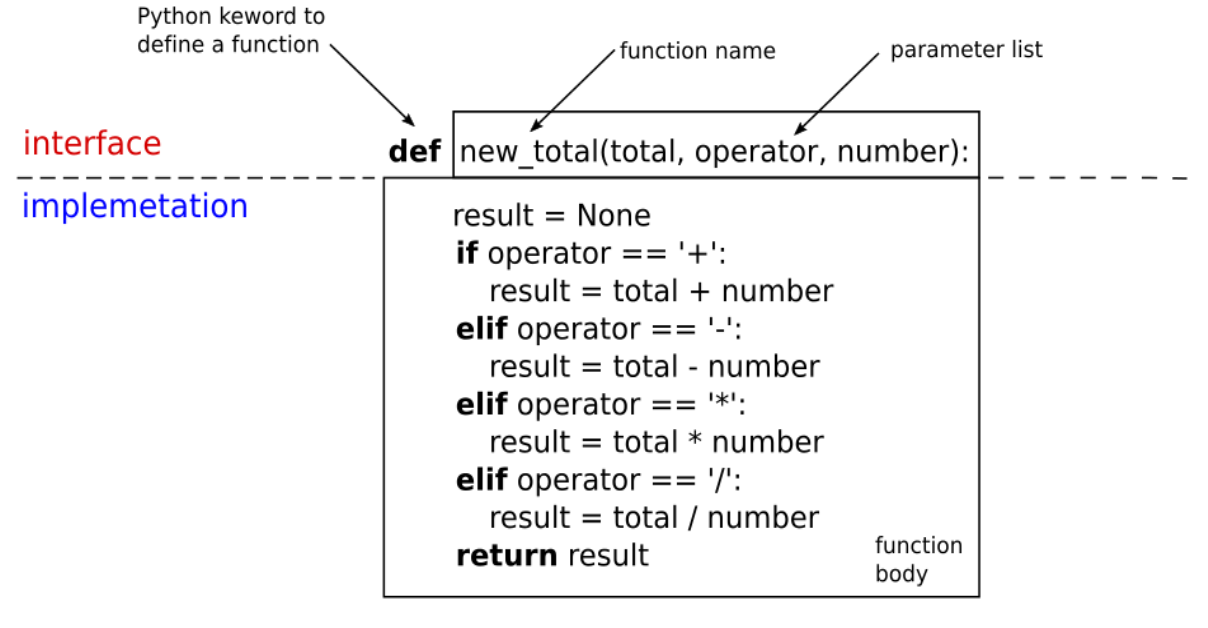
The function name, new_total, and its parameter list are visible to client
code that uses the function. The function's parameters may also be
referred to as its formal parameters or arguments. The function
body, in the function's implementation, is hidden from client code.
Inside the function body its parameters
become local variables. Such variables only exist while code in
the function executes and are then gone forever. We say the scope
of these variables is the function. Assigning a new value to a local variable
has no effect on anything outside the function even when an external variable
has the same name as the local.
The local variable result declared within the function is even more local than its
parameters: there is no way the value of result can be changed externally. However, when the function is called
by client code the values of the arguments to the call are passed
to the function initializing its parameters to the same values as the
arguments. Below old_total, operator and number are passed to new_total() and the return assigned to updated:
old_total = 101
operator = '+'
number = 7
updated = new_total(old_total, operator, number)
The arguments (old_total,
operator, number) are sometimes referred to as the actual
parameters of the call. The result of the function is returned to the
caller where it can be assigned to a variable, used in an expression or simply
discarded.
Placing the function in an expression
makes assignment to an intermediate variable unnecessary
cumulative = old_total + new_total(old_total, operator, number)
But if we write
new_total(old_total, operator, number)
The function
is called but its return value is not used. Doing this is pointless in this
case: new_total() has no effect other than returning
a value. Other functions may have useful side effects. The built
in function print() for example, sends
output to the screen.
The scope
of variables and functions
Python requires declare before use.
The scope of a variable or function is therefore from the point where it is
declared or defined up to the end of the file it is declared in. When another
file is imported variables and functions in that file will only be visible
after the import statement. There are two import options. An entire file or
files can be imported:
but when anything from the import is
referred to it must be prefixed with the file name
Alternatively, specific items from a file
can be imported and optionally given an alias:
from math import sqrt, pi
from math import sqrt as root, pi as pye
print(sqrt(2))
print(root(3))
print(pi)
print(pye)
Doing this the file name prefix is not
part of an item's name in the current file but all three options can be used
together.
When a file is imported any executable
code it contains is run to provide for initialization of variables in the
import. However, execution can be made conditional by putting code, and any
import directives, within an if statement:
if __name__ == '__main__':
inc_count()
import math
print(math.pi)
With the __name__ condition shown code placed within the if for testing or
debugging will only be run when the file itself is run not when it is imported.
Within the body of a function all items
whose scope it falls within are visible. Any external function can be called
and there is read only access to external variables. Optionally a function can
be given additional write access to a variable by declaring it global within
the body:
count = 0
def inc_count():
global count
count += 1 # read this as increment count by 1
Possibly useful for file initialization,
maintaining a counter for debugging or performance evaluation but generally to
be avoided, I think.
Function return values
A return statement in a function stops its further execution and the value from
any variable or expression that follows the return is passed back to the caller. There is of course a variation to
this no further execution rule. When the return is inside a try - finally block,
code in the finally part will be
executed come what may. This option can be left aside for the present.
There can be as many return statements in
a function as required each return representing a separate exit point. Using
this style new_total() can be implemented as
def new_total(total, operator, number):
if operator == '+':
return total + number
if operator == '-':
return total - number
# etc.
return None
When operator is not a '-' execution drops
through to the next test of operator, and so on. The elif: (else if) can be replaced with a simple if: there is no need to step over tests that follow when a return takes care of a success.
The return None statement is in fact redundant. When a function does not contain a return statement or return has nothing to
return, None is returned by default. You can see None being returned by a built-in function that only produces a side
effect and has nothing to return by executing print(print()).
However,
returning None, perhaps to show
that none of the conditions in a function was True, the return needs to be
explicit for clarity as to what is intended. By returning None we can write
result = new_total(old_total, operator, number)
if result != None:
... # some actions
else:
... # some other actions
Because None is logically equivalent to False in Python, we could write if result:
... but doing that is probably going to be wrong. A
zero value, integer or floating-point, also has a logical equivalent of False so the else actions will be
selected for all these cases. If that is the requirement then a remark in the
code to explain this is essential but that will mean just as much typing as
putting both conditions into if not (result == None or result == 0):.
Using single or multiple exit points
The opinion that a function should only
have a single exit point is sometimes seen. This idea probably dates back to a
very long time ago and supporters of old style Pascal. At that time Pascal was a language from academia
that attempted to promote structured programming by enforcing a single exit at
the end of a function, as opposed to C a language designed to cater for a specific range
of needs in real world programming.
As far as I can see a single exit has nothing to do with
structured programming. Execution in a function with
multiple exit points follows the form of a tree. In an equivalent with a single
exit point execution tends to the form a graph with nodes linked back to the
trunk, an altogether more complex structure. Introducing variables only
required to hold a return value until the end of the function introduces more
clutter and room for error.
The only advantage of a single exit was
simplification of resource deallocation by putting it at a single point, a
non-requirement when try - finally and
garbage collection is available. Go for simplicity and clarity over opinion with no logical basis and
use single or multiple exit points as indicated to get these requirements,
maybe?
Mutable and immutable
All the types we have looked at so far,
integers, real numbers and strings, are strict values. Such values are immutable:
they cannot be modified. Changing the value of the number 2 to make it 3 so all
twos in a program become threes is an obvious absurdity. It should not be and
is not allowed. We can change the value at a variable by assigning a new value
but the value itself is inviolate.
This is not the case with all types. Some
types are mutable and allow their content to be changed. When an
instance of one of these types is assigned to a variable a reference to the
instance is assigned. Assignment from that variable to another variable copies
the reference and both variables now refer to the same instance.
Not surprisingly modifications to an
instance from one variable are seen from all the variables that hold a
reference to it. Similarly, when a reference to a mutable type is passed as an
argument to a function, modifications to it as a local variable are reflected
to all other references. Some locals are more local than others.
The built-in type list is mutable. It supplies a sequence of any type and elements can be
modified by indexing into the list and assigning new values. In common with all
similar Python types indexing is zero based, the first element is at index [0]. For example:
def increment_elements(numbers_list):
index = 0
for number in numbers_list:
numbers_list[index] = number + 1
index += 1
a_list = [1, 2, 3, 4]
increment_elements(a_list)
print(a_list)
output: [2, 3, 4, 5]
As can be seen
modifications in the function increment_elements are seen from the variable a_list. Each iteration of the for loop
assigns successive elements of the list to num. The loop can be made slightly neater by using the built-in
function enumerate that returns both the element and its
index:
def increment_elements(numbers_list):
for index, number in enumerate(numbers_list):
a_list[index] = number + 1
The enumerate() function complies with the single return rule by returning a tuple. The tuple is unpacked
transparently to the variables index and number.
A tuple is similar to a list - elements have a specific and usually a meaningful
order, but a tuple is immutable once created.
Summary
Here we have looked at the usage and
structure of functions and the scope of entities within a program including local
and other variables. Algorithms 4 looks at functions with an indeterminate number of parameters. Lazy evaluation and closures will be considered in Algorithms 5.
[Algorithms 3: Functional integrity (c) Martin Humby 2015]