Although the Ancient Greek mathematicians discovered an enormous amount about geometry, in modern times a number of rather nice facts have been found that the Greeks didn't know about. One of these is Bottema's Theorem, named for Oene Bottema, a Dutch mathematician of the 20th century. It goes like this
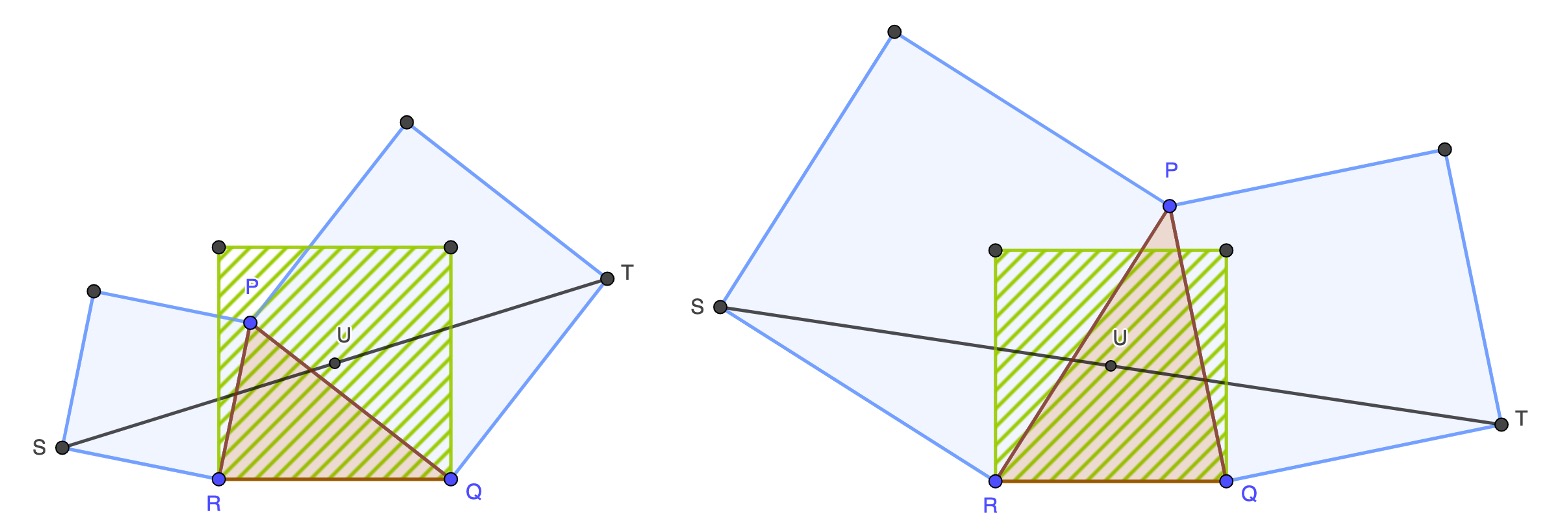
Suppose we have a triangle, PQR in the diagrams, and draw squares on two of its sides as shown. Draw a line joining the two vertices of the square that lie opposite to the vertex P and mark the midpoint U of the line that joins them.
Then the midpoint lies at the centre of a square resting on the base of the triangle and rather unexpectedly this is true wherever we move move the vertex P. The diagrams above show two positions of P and you can see that the position of U is indeed the same in both cases.
There are quite a few websites that discuss the theorem and give proofs, and there are also some nice animations and YouTube videos that demonstrate the fact that the midpoint is independent of P's position.
There are also some published variations on Bottema's theorem, but here is a neat one one I discovered by chance and which I haven't seen anywhere and which is new, to me at least.
Bottema's theorem works not just for squares but for any regular polygon with an even number of sides. For example, here is an example where the polygons have six sides.
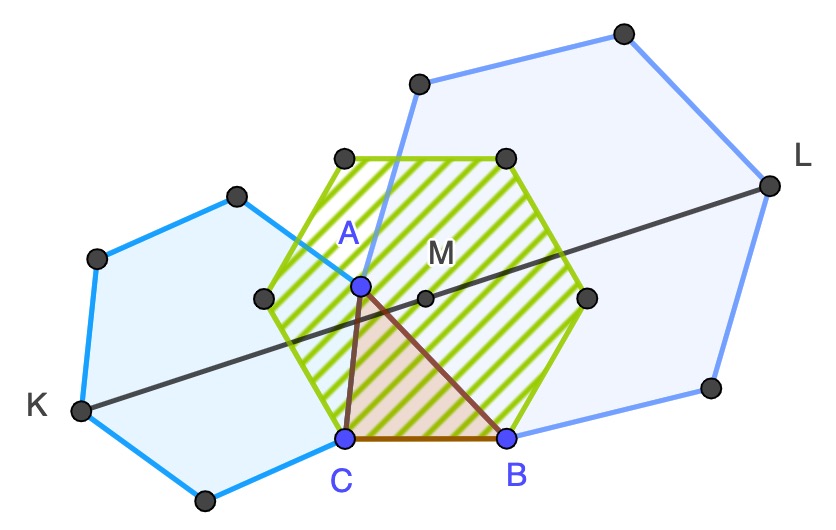
Notice that the midpoint M is now the centre of a third hexagon, rather than a square, resting on the bases of the square, and as with the square case the position of the midpoint does not depend on the position of vertex A.
If we instead erect octagons on the sides of the triangle then the midpoint will again be independent of the location of A, and will be the centre of an octagon resting on the base of the triangle. We can construct analogous configurations for any even number of sides, and the midpoint will always be fixed in the same way. I think that's rather neat and I was pleased when I discovered it.