Knock-Knock!
Who’s there?
Knock-Knock!
Who’s there?
Knock-Knock!
Who’s there?
Knock-knock!
Who's there?
Irma.
Irma who?
Irma dreaming of a White Christmas!
Just saw this motivation video that began
But if that is true we will never be able to find anything impossible. So finding something impossible will be impossible.
We were taught in school that the 'X' here is being used to represent first letter of Χριστός, Christós, the Greek for Christ, and so Xmas is just short for Christmas. This explanation certainly seems to be true and until tonight I never gave much thought to how long the abbreviation has been in use or why it was adopted.
The OED gives a citation from 1551 using the form X'temmas (which makes it clear that we are dealing with an abbreviation). By 1660 we have Xtmasse and by 1721 the modern form Xmas had evolved.
But from the Etymonline website we can get a little further information. The Anglo-Saxon Chronicle of about 1100 uses the form Xres mæsse and apparently an in Old English an abbreviation for Christ was Xr, or interestingly Xp, which resembles the fist two letters Χρ of Χριστός. So if things had gone slightly differently we might have ended up with Xpmas and talked about ex-ar-mas cards.
What I haven't been able to find out so far is whether Xmas is peculiar to English or similar abbreviations are found in other languages.
I've often heard this expression, which I took just to mean a sort of proverbially bad phrase book. But to my surprise it turns out to be a real book.
Its true title was O novo guia da conversação em portuguez e inglez, "The new conversation guide in Portugues and English", published in 1855, but later dubbed 'English As She As Spoke" because of the startling phrases to be found in it. The section Idiotisms and Proverbs gives a flavour of the contents:
The necessity don't know the low.
Few, few the bird make her nest.
He is not valuable to breat that he eat.
Its are some blu stories.
Nothing some money, nothing of Swiss.
He sin in trouble water.
A bad arrangement is better than aprocess.
He have a good beak.
In the country of blinds, the one eyed men are kings.
To build castles in Espagnish.
.. and so on. You can see this kind of stuff could get you some funny looks.
The general view is that the author had a Portuguese to French phrase book and a French to English dictionary, but did not speak English, so he picked a selection from the phrase book and then used the French to English dictionary to convert the French to English word by word.
French phrase book French-English dictionary
Portuguese phrases ----------------------------> French ---------------------------------------> English (sort of)
The original French phrase book was fine but the second stage, done in a very literal way by someone who did not know the target language, produced absurd and comical results.This came up naturally in conversation and I found it quite hard to say. Try repeating it a few times
"My ex next door neighbour"
This is my new invention, which has many possibilities.
My brother photographed these teal a couple of days ago.

They are the smallest wildfowl species in the UK, weighing 300 or 400 g. Only 2,000 or so pairs breed here, but in winter nearly half a million birds migrate here from countries further north.
More dipping into really. It's Mathematical Puzzles: Revised Edition, by Peter Winkler. It's rather good, but I only stumbled across it by accident. Somehow (I can't remember how) I read a Guardian newspaper puzzle column and it contained this gem from Winler's book:
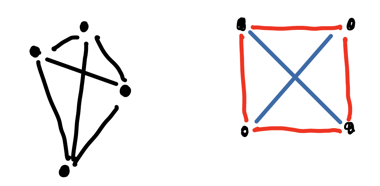
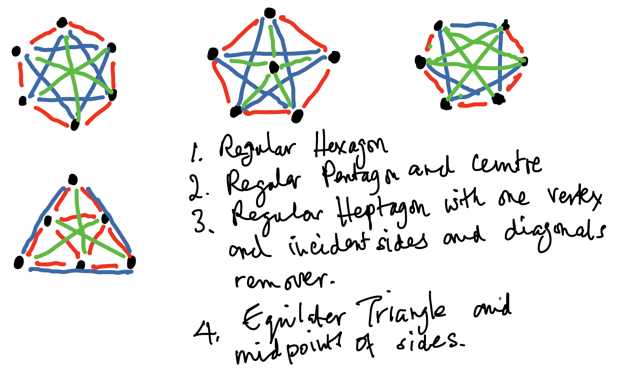
Find all the ways to arrange four points so that only two distances occur between any two of them.

As Merriam-Webster puts it [1]
What the #@*% Is a ‘Grawlix'?
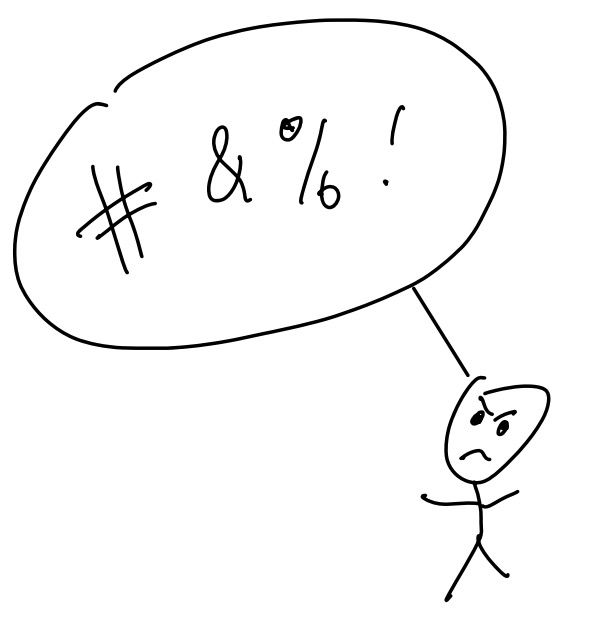
'Mistletoe' comes directly from Old English mistiltan. There's general agreement the -tan element means 'twig' and comes from an old Germanic root with the same meaning. The first element mistle is less straightforward. It's derived from missel, an old word for, well, mistletoe and the origins of this are less clear.
One theory is that it's from a root that meant something like 'urine' or 'feces', from the fact that mistletoe seeds are spread in bird droppings. If so it would be related to 'micturate', i.e. urination.
But many, many plants are spread by bird droppings, so why should mistletoe be singled out in this respect?
Another possibility that mistletoe is named for a related concept of something sticky, and this is plausible, because the berries of mistletoe are indeed very sticky and do adhere to birds' beaks and plumage and get spread that way.
Some support might be offered to this theory from the fact that the Latin word for mistletoe is viscum, which also meant something sticky, and from which we get viscous.
As an aside, the French for mistletoe is gui, and this is one of those words that has endured some surprising changes. It's said that viscum evolved first into wiscum, under Germanic influence, then into gwy, guy and finally gui. (At this point you might be wondering about 'gooey' but sadly there is no connection that we know of.)
The Ancient Greek word was ἰξoς and this seems to be cognate withe the Latin viscum; originally it would have started with a 'w' sound ϝιξoς but the ϝ letter was lost from Greek quite early. There are many other examples of words where the Latin and Greek were similar but the V or W disappeared from the Greek word, for example vicus 'village' and οἶκος 'house' (as in ecology and economy)
Two pictures here. Can you see what links the one on the left with the one on the right?

Image: Copilot designer
I got this problem from the book Mathematical Puzzles, A Connoisseurs Collection and thought about it in the shower.
Prove that given any 10 distinct numbers between 1 and 100 it is always possible to find two different non-overlapping subsets that have the same sum.
Here is my solution.
The least a subset can add up to is 0 and the greatest is 91 + 92 +... +100 = 955. The pair of subsets we want to prove exist can't have these values but that doesn't matter.
Imagine we have 956 buckets labelled 0 - 955.
Form each of the possible subsets of our 10 numbers, work out its sum, then put that subset in the bucket labelled with the corresponding number. For example the subset {1, 2} goes in the bucket labelled 3.
How may possible subsets are there? For any subset of our 10 numbers a given number is either in that subset or not, so we have 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 210 = 1024 possible subsets.
But 1024 is bigger than the number of buckets, which is only 996. Therefore at least on bucket contains two or more subsets, which must have the same sum.
This pair of subsets are different but might overlap, if so remove the numbers they have in common. This cannot empty either or both of the sets because if it did it would mean they were the same, or had different sums, and neither of those things is true.
Hence we have proved a pair of subsets with equals sums must always exist.
I asked Copilot for a long corporate-style answer to the classic Chicken Question and it came up with this. I think it did a pretty good job, probably because
a) there are lots of parodies like this out there for it to draw inspiration from and
b) it’s read millions upon millions of lines of corporate-speak in its training data.
Q. Why did the chicken cross the road?
A. In a strategic manoeuvre designed to optimise its geographical positioning and enhance its market presence, the chicken executed a calculated traversal of the thoroughfare. This initiative was undertaken to leverage the potential opportunities on the opposing side, thereby maximising its resource allocation and achieving a competitive advantage in the avian sector.
The chicken's decision to cross the road was predicated on a comprehensive analysis of the environmental variables and a thorough risk assessment. By engaging in this cross-road venture, the chicken aimed to capitalize on the untapped potential of the adjacent territory, thereby driving growth and fostering innovation within its operational framework.
This bold move was aligned with the chicken's overarching mission to expand its footprint and deliver value to its stakeholders. The crossing was not merely a physical relocation but a strategic realignment designed to enhance the chicken's long-term sustainability and profitability. Through this initiative, the chicken demonstrated its commitment to proactive market engagement and adaptive strategy execution.
In conclusion, the chicken's road-crossing endeavour was a testament to its forward-thinking approach and its unwavering dedication to achieving excellence in its domain.

Image generated by Copilot Designer
Frequentative is a term from grammar, one that I only learned about a couple of days ago while watching the Words Unravelled podcast. A frequentative is a word formed by appending the suffix -le or -er to a verb or noun to express the idea of a repeated action. Here are some examples with -le
spark -> sparkle
prick -> prickle
game -> gamble
daze -> dazzle
crumb -> crumble
fizz -> fizzle
scud -> scuttle
twink (same as wink) -> twinkle
wag-> waggle
This suffix derives from an old Germanic suffix with a similar meaning.
Here are some examples with -er. These are less clear cut sometimes, because the suffix can have other senses.
gleam -> glimmer
slide -> slither
flit -> flitter
The word frequentative sounded fairly modern to me, but in fact it is recorded in the grammatical sense as early as 1534, in Nicholas Udall's Floures for Latine spekynge selected and gathered oute of Terence
“Meet Antony. He used to be a cab driver”, said Tom exuberantly.
The London Eye, by Image Creator (2024)

“Sydney and I have been chums for absolutely ages”, said Tom frenziedly.

https://commons.wikimedia.org/wiki/File:Crouton_skibidis_next_to_an_ice_cube.jpg
'Crouton' and 'crystal' both ultimately stem from an ancient root that was something like kreus and meant 'freezing over' or 'crusting'. Crystals were thought in Ancient Greece (not unreasonably) to resemble frost, kryos, and from that was derived krystallos.
Related words are crust, crustacean, a whole series of modern words coined from cryo-, and, surprisingly, custard.

This image was generated by Copilot and it makes me laugh every time I look at it. I love the eager enthusiam on the cats' faces.
In mythology there are many divinities who ride in chariots drawn by exotic animals, but cats are unusual, although in Norse myth the goddess Freyja is pulled by a pair of cats. These are feisty beasts, as you can see in this illustration.

Credit: Ludwig Pietsch, 1865
Some sources say they are named "Bygul" and "Trejgul" but this is a little suspect, because there are Latin words Biga and Triga which mean respectively a two-horse and a three-horse chariot. So do the names reflect an Old Norse confusion about the meaning of the Latin words? Or perhaps a learned joke by a medieval scribe?
You can read more about bigae, trigae (and even quadrigae) in a fascinating article here.
“My job is studying social insects”, said Tom observantly.
This blog might contain posts that are only visible to logged-in users, or where only logged-in users can comment. If you have an account on the system, please log in for full access.