Yesterday was the one day in the year when the alphabet has only 25 letters.
Noel.
Yesterday was the one day in the year when the alphabet has only 25 letters.
Noel.
This is the solution to the problem posted at https://learn1.open.ac.uk/mod/oublog/viewpost.php?post=279732
When two dice are rolled there are 6 x 6 = 36 possible outcomes, all equally likely. However the information that at least one has come up six narrows down the number of possibilities to the 11 shown as crosses below.
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | x | |||||
| 2 | x | |||||
| 3 | x | |||||
| 4 | x | |||||
| 5 | x | |||||
| 6 | x | x | x | x | x | x |
A friend who I know to be reliable rings me up and tells me they have just rolled a pair of dice and at least one came up 6. What is the probability that the other one also showed 6?
This picture is from the cover of the February 1925 edition of Science and Invention. The author of the article on page 978 was Hugo Guensback.

Guensback's prescient article foreshadows by nearly 100 years developments that are only just starting to become common.

The 'teledactyl' sounds like a prehistoric winged reptile but is in fact a remote finger that mirrors the movement of the doctor's finger. Here is Guensberg's diagram of how the system might work.
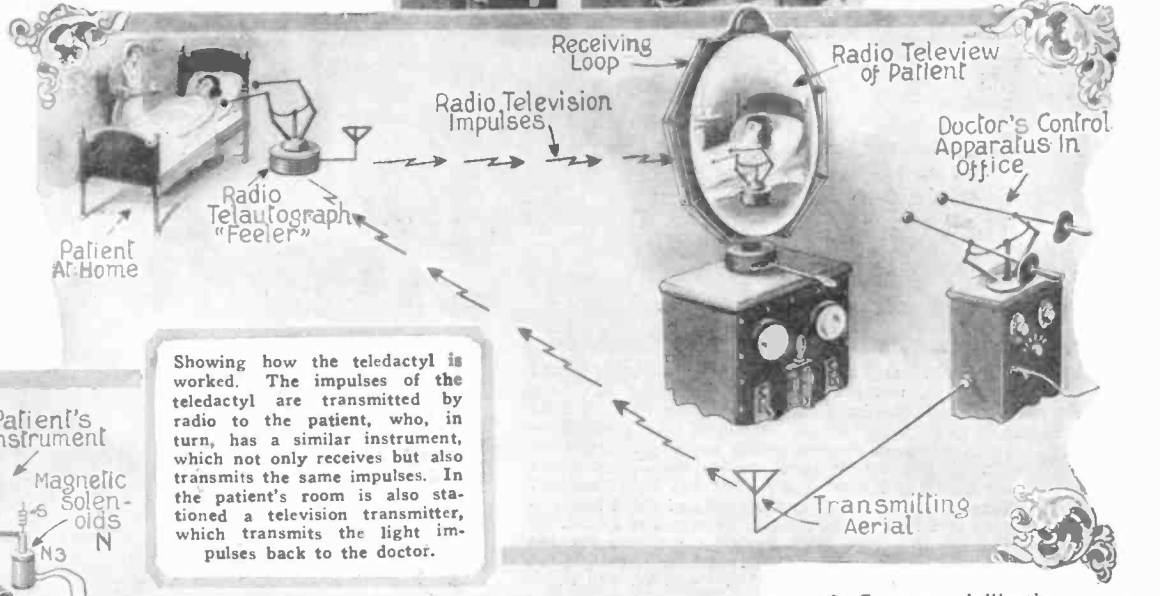
This is all quite well thought out and even in 1925 it might have been possible to build a limited proof of concept prototype in the laboratory but of course cost and technical issues would have made mass production impractical, and without a modern communications infrastructure such as the internet it would be very hard to make it work in practice.
Here is a link to the whole article, courtesey ofl worldradiohistory.com
https://www.worldradiohistory.com/Archive-Electrical-Experimenter/SI-1925-02.pdf

Generated by DALL_E from a photo of a hawthorn bush
Yesterday we went to a Christmas Tree Festival in the village church. There were about 30 trees from various local groups and organisations. Some were actual Christmas trees but others had been put together from various materials. They filled the whole church, and the effect was rather magical.

My Mother was very, cold towards me, but Father was aloofer. He was a bath sponge.
Once upon a time a Hare

Challenged Sooty

To a race.
The Hare got off to a flying start and soon Sooty, being only a glove puppet, was lagging badly. When the Hare looked back Sooty was nowhere to be seen.
So the Hare lay down for a nap.
You guessed it, Sooty came up from behind, passed the Hare, and reached the finishing post first.
In the papers next day the headlines readAn acronym is formed from the initial letters in a phrase, and can become a word in its own right. Scuba is a good example, derived from Self Contained Underwater Breathing Apparatus. People like acronyms; they are handy and memorable.
A backronym is the exact opposite. Starting from a word that looks as though it could be an acronym, we reverse engineer an origin, sometimes to be comical, but sometimes because an acronym is suggested that seems plausible and satisfying. And some backronyms are for serious purpose, as explained here
https://en.m.wikipedia.org/wiki/BackronymAs an example of the plausible type, it’s commonly said that posh comes from Port Out Starboard Home, in the context to sea travel to India, but I don’t believe there is any reliable evidence for this explanation. It always seemed fishy* to me.
A more modern backronym is rap = Rhythm And Poetry, which seems equally unlikely to be true.
And a really funny one is
* False Information Some Hand You.
Erm, what's the name of that French bread? I baguette.
These amazing plants look like something from a Gaugin painting. They were seen in the Jardín de Aclimatación de la Orotava, Tenerife which dates from 1788.
My Aunt died today.
And I can remember her;
Running across a sunlit field
With we three children in hilarious pursuit
Laughing at the wind in our faces.
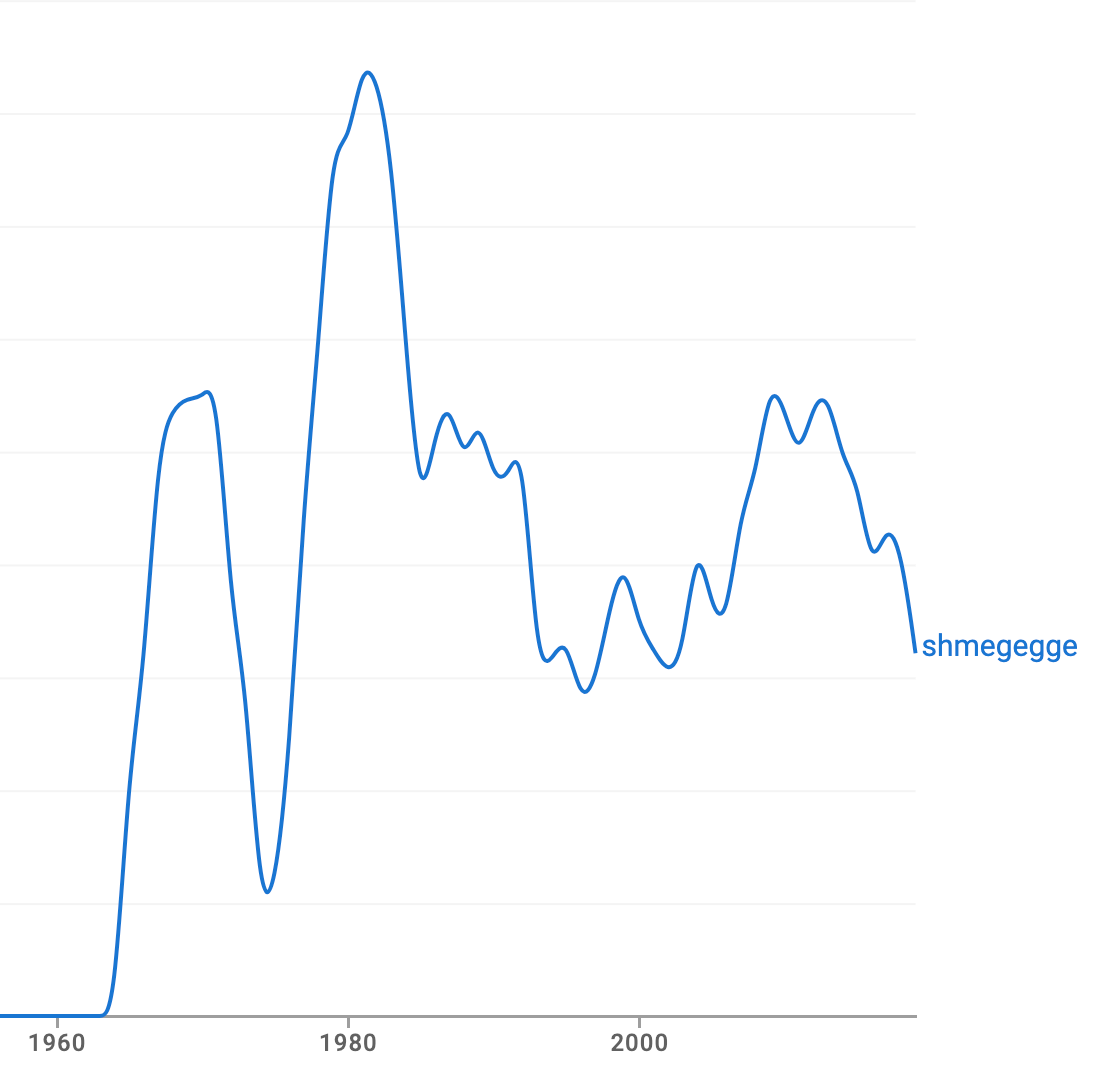
Yesterday i stumbled across this expressive word from Yiddish:
shmegegge
meaning baloney, nonsense, rubbish, as in "Don't give me all that shmegegge".
It's pronounced shmuhGEGee. according to the Oxford English Dictionary.
Here's the Google ngram. It's quite a recent word it seems, and is a bit less frequent than in the past. But why those high peaks? Was the word in. a film or TV show around those times? I'd love to know.
George Orwell I think it was that said Macbeth is a play about ambition.In this famous speech near the end of the play, Macbeth, facing ruin and defeat, meditates on the ultimate folly of human ambition.
Met a woman claiming to be the Roman goddess of crops. I was like really? You can’t be Ceres.
枯朶に烏のとまりけり秋の暮
on a withered branch
sits a crow
autumn nightfall
This blog might contain posts that are only visible to logged-in users, or where only logged-in users can comment. If you have an account on the system, please log in for full access.