We found this newt in the garden just now.

As far as I can tell it is a Smooth New, AKA as a Common Newt. This individual is unusually dark on its upper side, but I'm pretty confident in my identification. It's a beautiful little creature.
We found this newt in the garden just now.

As far as I can tell it is a Smooth New, AKA as a Common Newt. This individual is unusually dark on its upper side, but I'm pretty confident in my identification. It's a beautiful little creature.
“What’s that chicken doing in the road?” asked Tom crossly.
It's quite surprising - to me at any rate - that if we take any positive number whatsoever, there is always a prime number that starts with the digits of the number we picked. In fact there are an infinite number of such primes.
I wrote a Python program that lets us input a number and searches for the first prime beginning with the number we entered.
Say we take Einstein's birthdate, 14/03/1879. Write this as 14031879 (which is not itself prime, it's divisible by 3).
Entering this into the program yields 140318797, which as you see starts with the famous scientist's birthdate, and has no divisors other than itself and 1, so it's prime.
Here's another example, this time a random number (I suppose) - the National Lottery jackpot for 14/09/2024, which was 21 27 38 47 49 55. Running the program and entering 212738474955 we get 2127384749557.
By tweaking the program we can get a list of the first few primes that start with the lottery number.
2127384749557
21273847495583
21273847495591
212738474955233
Fascinating!
 I'm rather pleased with a couple of little olive trees i've just acquired. They have lots of olives on them, I was surprised. I wondered if we could eat the olives, and it seems the answer is yes, but they will need to ripen a bit more, and then be cured, in water or brine, to stop them tasting bitter. It's a bit fiddly but I think it will be worth the effort.
I'm rather pleased with a couple of little olive trees i've just acquired. They have lots of olives on them, I was surprised. I wondered if we could eat the olives, and it seems the answer is yes, but they will need to ripen a bit more, and then be cured, in water or brine, to stop them tasting bitter. It's a bit fiddly but I think it will be worth the effort.
My trees are very small and only youngsters, and that set me thinking about how old olive trees can live to be. This one from Ano Vouves in Crete is claimed to be 2000 - 4000 years, so it stretches back to antiquity.

You can read more about it, and take a virtual walk round it it, at the web site here that I pulled its picture through from.
This is the proof of the question I posted at https://learn1.open.ac.uk/mod/oublog/viewpost.php?post=285828
Here's a sketch

Chord AB is a typical chord passing through a fixed point P in the interior of a circle. Point M is the midpoint of AB and I have drawn in (shown dotted) the two line segments joining P and M to O, the centre of the circle.
By symmetry, the line MO joining the midpoint of the chord to the centre must be perpendicular to the chord. So triangle MOP is right angled, and PO is its hypotenuse.
By the converse of Thales' theorem the hypotenuse of a right angled triangle is the diameter of a circle passing through the three vertices of the triangle, and the centre of the circle is the midpoint of the hypotenuse, N in the diagram above.
The diameter and centre of this circle are fixed by the position of P and O and midpoint M must be on this circle for any chord through P, which is what we wanted to prove.
For information about Thales (fl. 626/623 – c. 548/545 BCE), who seems to have pursued many scientific, mathematical and philosophical interests see here
Escalators. They have their ups and downs.
Richards often get called Dick - my father always did - but I never really thought much about how Richard could translate to Dick. But yesterday I was reading about how studying pet names for people can help with etymological research and came across the idea of "rhyming nicknames", the result of a process like this
name -> shortened form -> rhyming nickname
So we get Richard -> Rich -> Dick, it's as simple as that
Obviously I knew about ordinary shortenings and diminutive pet names (e.g. Thomas -> Tom ->Tommy) and I've also been intrigued by the fact that names whose shortened form would end in 'R' are modified to end in 'L', e.g. Terence becomes Tel and Harold becomes Hal (probably because "Ter" and "Har" don't trip off the tongue so easily). Another such is Chas.
We can also shorten names from the other end, so Richard can be Hud and William can become Liam for example.
However I hadn't really twigged about the rhyming nicknames but there are lots of them and they seem to have been popular in Middle English. Here are some common examples:
Richard (again) -> Rick -> Hick
Edward -> Ed ->Ted (or Ned)
William -> Will -> Bill
Here's a surprising one:
Margaret -> Molly -> Polly
or
Margaret -> Meg -> Peg
Finally we have
Robert -> Rob (possibly via Robin, a diminutive) -> Bob (or Hob) and Hob is the first element in Hobgoblin, a kind of mischievous elf. Robin Goodfellow, a kind of goblin and Puck-like character, became Hob the goblin.
Goblin is interesting in itself, it seems to be from the same root as German Kobold, and became the name of Element 27. Element 28 another troublemaker.

There's an oldish joke, I can't remember where I came across it first, that runs as follows.
Q. What happens to naughty sunbeams?
A. They get sent to prism. But they only get a light sentence.
I was thinking about this joke and the fact that the prism refracts the light, and I wondered about the word origin of the word refraction. I looked it up and was quite surprised. It seems to go back to Latin refract, the stem of the past tense of refringere, 'to break or deflect', and be related to fragment and fraction.
The Online Etymology Dictionary goes further and traces it back to a Proto-Indo-European root *bhreg-, 'to break' and that is also the origin of 'break', which is thus a word that has changed little in more than 5,000 years.
Even more surprisingly the same root is probably connected to 'breach', 'brake' and 'brick', as well as a host of other words, see https://www.etymonline.com/word/frangible#etymonline_v_11872.
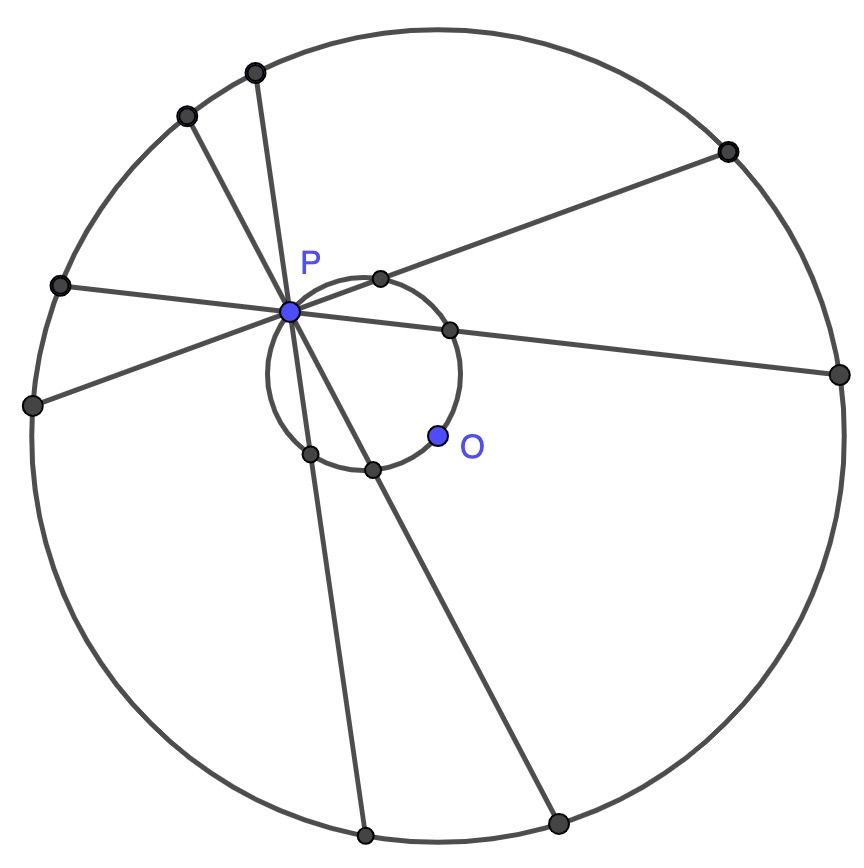
Given a circle centre O and a point P in its interior, the midpoints of all the chords passing through P lie on a circle, which also passes through P and through O.
"Mirrors don't lie", said Tom reflectively.
My title describes something most of us have known about all our lives without realising it.
Why do 'hip hop' and 'ding dong' sound right, but 'hop hip' and 'dong ding' sound wrong somehow? It's not just familiarity, there is a rule at work, as we shall seen. If I invented a new expression 'squop-squip' it wouldn't sound as satisfactory as the alternative 'squip-squop', because the first version doesn't follow the rule, whereas the second does.
Reduplication is when a word is repeated two or more times. In English there are several kinds of reduplication, for example it can be used to amplify the sense of a word, so 'very very' is stronger than simple 'very' and 'big big' is stronger than just 'big'.
Rhyming reduplication is also very common: higgledy piggledy, silly billy, willy-nilly, Humpty Dumpty, raggle-taggle, easy-peasy (lemon squeezy), teeny-weeny, fuddy-duddy and so on.
Ablaut reduplication is a form of reduplication following a pattern called ablaut, in which semantically related words coming from the same root keep the same consonants but vary the vowel sounds in a predictable way. A classical example in English is sing, sang, sung. Notice that if you say these words aloud, you say the first at the front of the mouth, the second further back, and the third at the back of the mouth.
We have many expressions like; tip-top, tick tock, flim-flam, pitter-patter, jim-jam, and they pretty well all follow the ablaut pattern, with the first part being a higher vowel from front-of-mouth, and the second a lower vowel from further back. We even have some examples with three elements, such as tic-tac-toe and bish bash bosh.
This ablaut pattern is thought to be inherited from the ancient and lost language that is the ancestor of moist European and West Asian languages today. This language had no written form that we know of, and no longer exists, but has been extensively reconstructed from its more recent descendants.
Someone asked on Quora how, given two concentric circles, we can construct a square having two vertices on one circle ands two on the other.
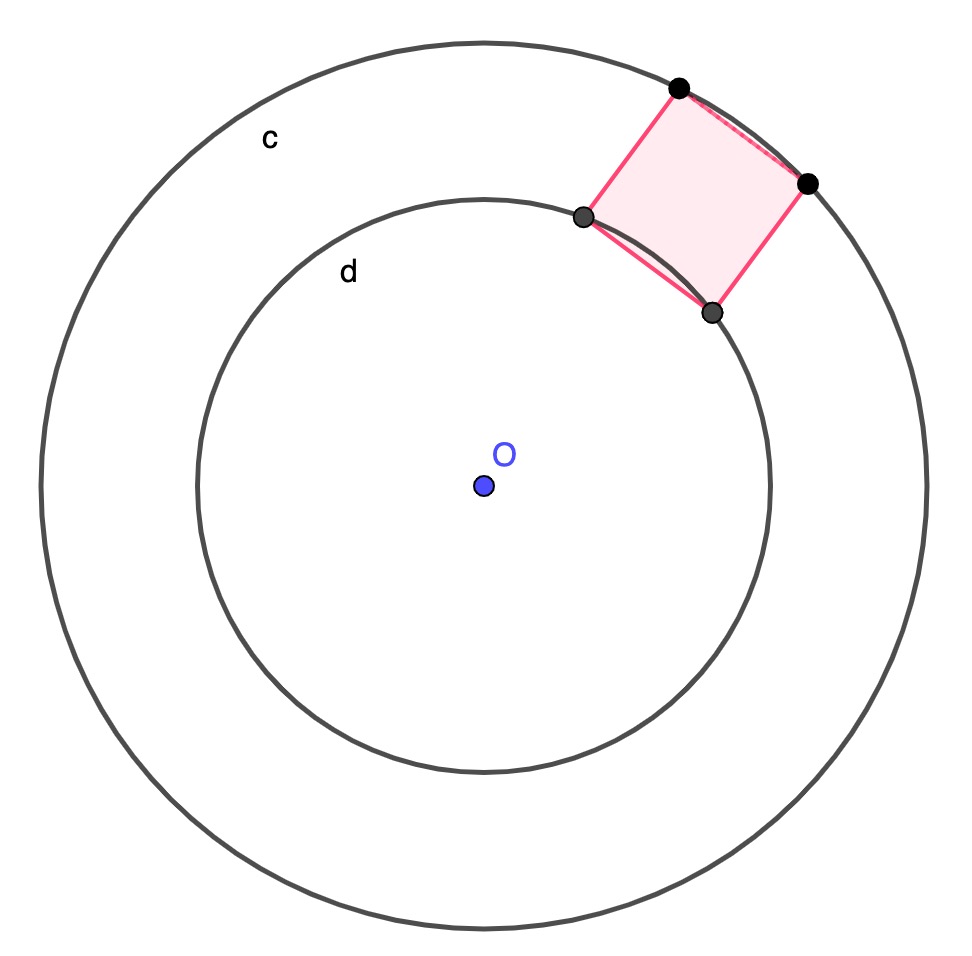
I think this was answered by the notable Alon Amit, but I deliberately haven't looked at his solution yet. Here is my solution.
Choose a point A on the outer circle c and rotate c through 90 degrees about A, to give circe c', shown fotted.
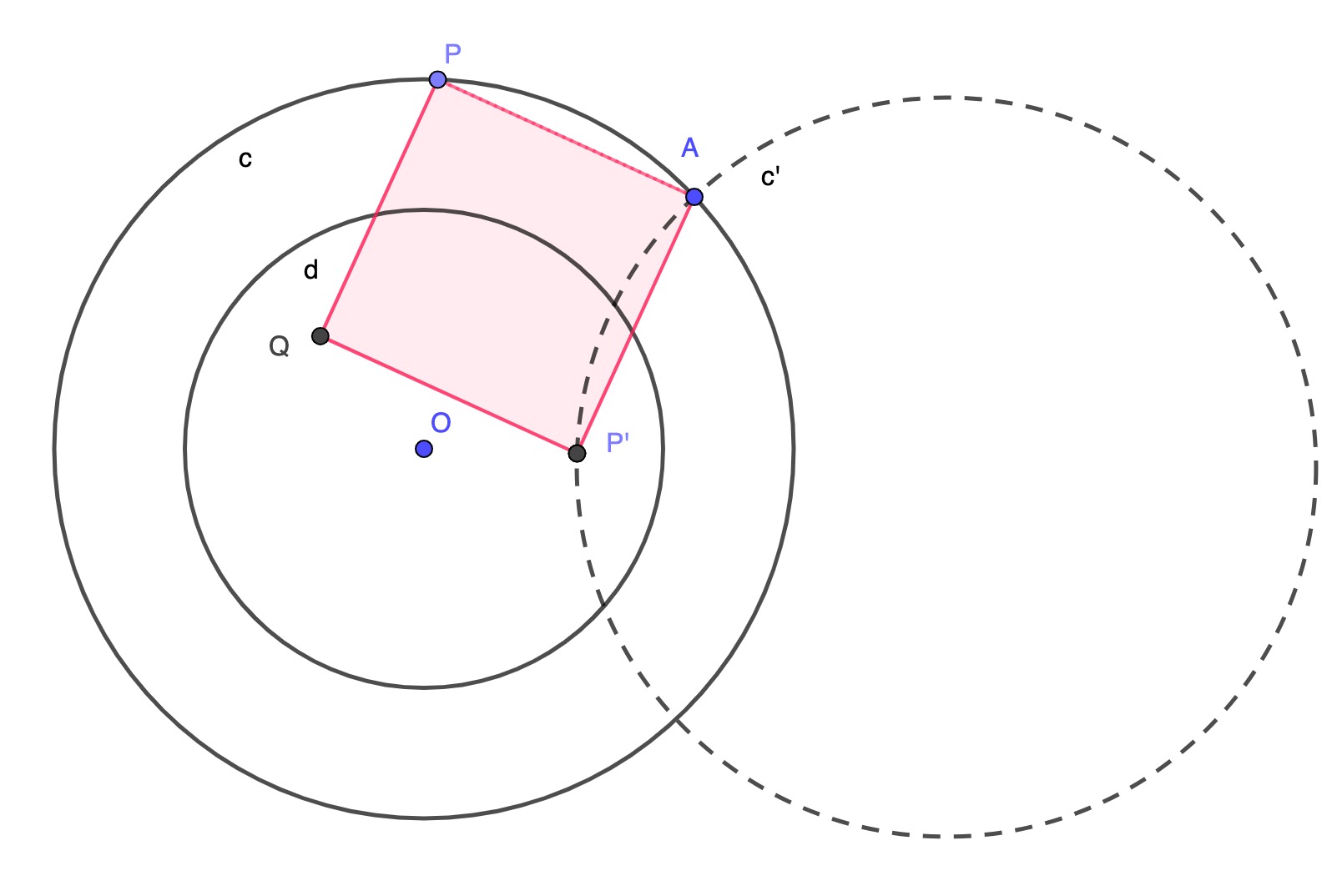
Because c' is the rotated image of c, any point P' on c' is the image on a point P on c, and any point P on c is the inverse image of a point P' on c'. Angle PAP' is a right angle, from the construction, and length PA = length P'A by the same reasoning. This defines the square PAP'Q with two vertices on c, shown shown shaded.
All we now need to do is choose P' to be the point where the dotted circle c' intersects the inner circle and we obtain the required square, since Q must lie on the inner circle by symmetry.

Of course if the inner circle is too small this doesn't work, because the dotted circle and the small one don't intersect. The limiting case is when the inner radius is ~ 0.414 of the outer one.
A friend photographed this astonishing piece of street art outside Paddington Station. With the aid of Google Lens I found it is "Wild Table of Love", by Gillie and Marc.

Images Creatine Commons: https://www.geograph.org.uk/photo/5685222, https://commons.wikimedia.org/wiki/File:QS_Toffee_Penny_RPMG.jpg
"There's a nail in that tyre", Tom said flatly.
¨I’m a lawyer”, said Tom briefly.
There is a classic Tom Swifty joke - I don't know who thought of it first - that runs as follows
"You must be my host," Tom guessed.
This is rather neat, especially given host and guest turn out to closely related words. In the reconstructed Proto-Indo-European tongue believed to be the distant ancestor of many languages alive today they were the same word, which meant both host and stranger/guest, and was something like ghosti.
This ancestor language predated the invention of writing, so this is just something we have worked out from the evidence of more recent languages that were written down (for example Latin and Old English etc.), and of course the languages spoken at the present time. However scholars are fairly confident our reconstruction is broadly right.
The original word has come down to us through different routes and so host and guest have separated in English, but in some languages the equivalent word seems to retain the dual sense; for example Italian ospite.
I suppose we could say this is a contronym (see here).
It's interesting to consider that back in the day, we'd never heard the expression "Back in the day".
My grandad used to say, “No news is good news.”
He was a lovely man, but a useless reporter.
The latest video in the excellent series Words Unravelled, with RobWords and Jess Zafarris, is devoted to "contronyms and other 'onyms'". Most people are familiar with words such as synonym, antonym, pseudonym, acronym, but I hadn't met contronym, which means a word with two meanings that are in some way opposite. For example I might sanction someone, which would mark my disapproval, but I might also sanction a course of action, which would mean I gave it my approval.
The suffix -onyms is from the Greek for name, and there are quite a few -onyms apart from the ones about. Rob and Jess discuss a whole range of other other interesting -onym words.
I thought I'd explore a bit further and was intrigued to find a number that describe names for physical features of the landscape, each formed by taking an Ancient Greek word for the feature in question and adding -onym. These all refer to proper names, e.g. Helvellyn is an oronym, The Grimpen Mire is a helonym, The Black Forest a drymonym, and so on. Here are the words I managed to find.
agronym – field
anemonym – hurricane
drymonym – forest
helonym – swamp
hydronym – sea
limnonym – lake
oronym – mountain
spelonym – cave
Here are some things you might find in a cycene. Although the majority of words in English today have come from French, Latin, and other non-Germanic languages, most of these familiar domestic objects still have names very similar to their Old English equivalents. See if you can recognise what the objects are.
beod
bolle
cietel
cnif
cucler
cuppe
disc
hlædel
ofn
panne
sife
stol
"Will you marry me?", asked Tom engagingly.
This blog might contain posts that are only visible to logged-in users, or where only logged-in users can comment. If you have an account on the system, please log in for full access.