
Personal Blogs


Most sources say "Windermere" is from ON male name Vinandr and OE mere, so it would mean "Vinandr's Lake". A bit more digging suggests Vinandr is a dithemic name composed of two elements - very common in names of Germanic origin. "AI Overview" suggests the elements here are wig = battle and nand = brave. Another name with the wig element in is Wystan.
I was marking a programming exercise that involved taking account of leap years, and I realised I didn't know what the term was derived from: why "leap"? So I looked it up. The origin is not certain but the most likely explanation is as follows.
As you know, it was realised from ancient time that a year is not exactly 365 days but a bit over, about six hours. At one time this was ignored, but doing so caused problemsas time went by, and Julius Caesar introduced a reformed calendar in which every fourth year would have an extra day, which would compensate for four lots of six hours, so making the average length of a year 365.25 days. This extra day was in Latin a bissextus.
Medieval Christianity celebrated a series of feasts, or festivals, some moveable (e.g. Easter) but others like Michaelmas, which falls on on 29th were fixed. (Of course many are still celebrated today but I think a lot of saints' days were included and we are less aware of these nowadays.)
In successive years the day of the week on which a fixed festival falls will advance one day per year, so if it falls on Monday this year, then next year it will be on Tuesday except, except...
If the current is a bissextus and the festival is on or after 29th February, a day will be skipped and the day of the week will advance by two days. We have leaped over a day!
The OED gives this rather nice quotation from the 14th century:
Of course the calendar we use today takes into account the fact that six hours is an overcompensation, so if the year is a multiple of 100 we skip the extra day, except that now we have gone a tiny bit too far the other way, so if the year is divisible by 400 we reinstate the extra day. With these tweaks things should be fine for about 20,000 years.
Robins hop but Pigeons walk.
What determine the style of locomotion a bird species favours? Some quick online research threw up three factors that are thought to predispose a species to one mode or the other, although it is easy to find exceptions in each case.
1, Size
A small short-legged bird may travel further for a given amount of energy by hopping rather than walking. But some big birds hop, e.g.Toucans, and some small birds such as Skylarks walk.
2. Family tree
Birds that of closely related species tend to use the same form of locomotion. But while most members of the Crow family walk, Jays hop. And Emus and Penguins both walk but are not closely related.
3. Habitat
Birds that live in trees and bushes can get about best by hopping from branch to branch as opposed to walking along branches and twigs. However Parrots often live in trees but walk, not hop. And Dunnocks (AKA Hedge Sparrows) seem to live mainly on the ground, but are hoppers.
Many birds can both hop and walk, and while I was watching my garden birds I noticed that Blackbirds fall into this category: our resident Blackbird ("Blackie" as we imaginatively call him) was hopping along and suddenly broke into a run.
Most of this information came from the sources below.
https://www.newscientist.com/lastword/mg24833051-100-are-birds-that-walk-more-advanced-than-those-that-hop/
https://www.sciencefocus.com/nature/why-do-some-birds-hop-and-others-walk
Then as the socks are drawn one by one from the draw it is possible that socks 1 and 2 match, socks 2 and 3 match, and so on, up to socks 2n - 1 and 2n. In all there are 2n - 1 possible pairs of consecutive socks whose colour could match.
In each consecutive pair once the colour of the first sock is known there is then a 1/(2n - 1) probability that the next sock with be the same colour, or in other words the mean expectation of the colours matching is 1/(2n - 1).
But this applies to all 2n - 1 pairs and by the principle known as linearity of expectation we can find the overall expectation simply by adding the 2n - 1 individual expectations. But (2n - 1) x 1/(2n - 1) = 1 and so we conclude the expected number of matches is 1, whatever the number of pairs of socks in the draw!
I wrote a Python program and ran it, and sure enough as predicted the result is always close to 1.
n = 20trials = 10000
sox = list(range(n)) * 2
matches = 0
import random
for i in range(trials):
random.shuffle(sox)
for j in range(2*n - 1):
if sox[j] == sox[j + 1]: # do socks match?
matches = matches +
print('Mean =', matches/trials)
Suppose I pull socks out one at a time, with my eyes closed, until the draw is empty. How may times can I expect two consecutive socks to be the same colour?
I came across in the Times "Word watch" (Times 2, 01/05/25). According to the OED it originally meant "an idler who stares at length at activity on a canal", and by extension someone who stares at anything for a long time.
The OED classifies it as a dialect word and cites the Glossary to Bradshaw's Canals & Navigable Rivers Eng. & Wales (1904), which suggests a Lake District origin. Here is the entry, which I located with the help of Google Books

I thought I'd see if I could find out more about the origin, so I tried asking DeepSeek AI and it suggested the first print appearance as being in "The Folk-Speech of South Cheshire" by Egerton Leigh. This seemed promising! After some digging I located such a book and was getting quite excited - but alas! gongoozler was not there, DeepSeek was wrong.
The OED's summary is that the word of unknown origin, but does offer a tantalising third possibility –
"... compare Lincolnshire dialect gawn ‘stare vacantly or curiously’, gooze (also goozen) ‘stare aimlessly, gape’."
– and perhaps that's the best guess we have.
This sounds very similar to the name of the famous Battle of Marathon (490 BCE), at which an Athenian army, with a smaller contingent from Plataea, resoundingly defeated a much stronger Persian force, in an encounter often seen as the epitome of a brave defence overcoming a powerful and aggressive adversary.
And indeed the place is named after the plant. I once visited Marathon and there wasn't a whole lot to see really, and I can't remember any fennel, but the place was noted for it in the 5th century BCE. The word marathon itself has a long history, because it is attested in a tablet or tablets from Mycenaean times, so around a millennium earlier than our battle. The tablet was written in Linear B script, not Greek characters, although the language was early Greek, and the word is transcribed like this
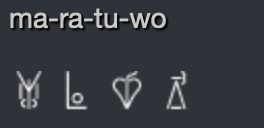
To return to the story: the Athenians had sent a runner, Pheidippides, to the other pre-eminent Greek city at the time, Sparta, to ask for assistance, but Sparta was in the middle of a solemn religious festival whoch prevented them for responding straightaway.
There was not enough time to wait for the delayed Spartan help to arrive, so the Athenian army and 1000 soldiers from Plataea fought alone. The Greeks attacked the Persians and eventually won, against the odds.
Now although Pheidippides' epic run seems to have been to Sparta, as described above, in time a second version of the story emerged: that Pheidippides ran instead to Athens, bearing news of the victory. Marathon to Athens is - well, about the length of a modern Marathon. When the Olympic Games were resurrected in 1890, a race over this distance was included, although it had not been part of the ancient Games.
Now -athon has become a productive suffix denoting some activity taking place over an unusually long distance or time, so in the OED you can find danceathon, skate-a-thon, cut-a-thon (hairdressers) and schmoozathon, and Collins gives walkathon, drinkathon and sale-a-thon as examples.
Here's another nice geometrical theorem. I hadn't seen it before today but it seems it's usually called Thébault's problem II and is credited to Victor Thébault (1882–1960), a mathematician who published over 1000 problems
Here's how it goes (this is a slight extension of the original problem, which had a square where the following requires only a parallelogram). Given a parallelogram ABCD as shown, erect equilateral triangles on two adjacent sides. Then the two free vertices of those triangles together with the vertex of the parallelogram opposite form an equilateral triangle.
The following is my proof. I haven't looked at any published ones, but I'm sure this is one of the standard ones and I imagine we could use complex numbers quite nicely as well, but this uses only ideas that would have been familiar to Euclid.
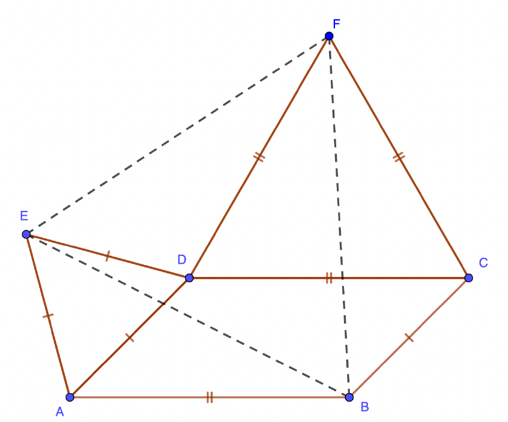
In this diagram there are two different lengths, marked with | and ||. Call these L1 and L2 and suppose the angle BCD is α. Then using the properties of equilateral triangles (all angles are 60) and parallelograms (adjacent angles add up to 180) we can mark in a series of angles.

The angle EDF is 60 + α by subtracting the other three angles at D from 360.
Now if we consider triangles EFD, FCD and BAE, we see they all have an angle of 60 + α between sides of length L1 and L2, which means these are all congruent and it follows immediately that the three dotted distances are equal and BEF is equilateral as claimed.
Thébault's theorem has attracted some deal of interest, because it is so neat and quite simple, but seemingly was not spotted for over 2,000 years. It has ben generalised at least twice, most recently in 2019, see The Mathematical Gazette, Vol. 103, No. 557 (July 2019), pp. 343-346.
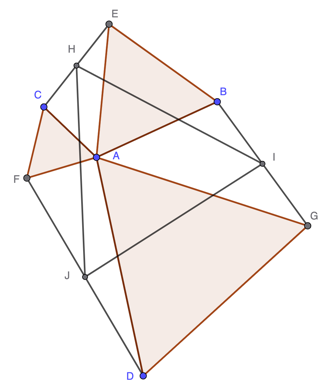
Suppose equilateral triangles ABE, ACF and ADG share a common vertex A as shown. Then the midpointss of the segments EC, FD and GB form the vertices of an equilateral triangle.
The special case where points BECFDG lie on a circe centred at A was proved by Alon Amit (April 5 2020) in response to a question posed on Quora:
A hexagon is inscribed in a unit circle such that three alternate sides are of unit length with the other three arbitrary. Connect the midpoints of the three arbitrary length sides. Can you prove those points form an equilateral triangle?
Amit's clever proof, using complex numbers, does not in fact depend on the points lying on the unit circle and holds as long as we have the configuration in the figure above, and this more general case is even more surprising than the original version.
I've just helped towards a Kitty's expensive dental bill. I was happy to do it, because I'm an Ailurophile. The word is relatively modern (1914) and comes from Ancient Greek ἀίλουρος "ailouros" = cat, which is thought to originally mean something like "wavy tail", rather poetic to my mind. A somewhat earlier term for a cat lover was Philofelist, dating from 1843.
A dog lover is a Cynophilist, or Cynophile, from Greek κυνος "kynos" = dog, from Proto-Indo-European kwon, which is also the root of words such as hound, kennel, and canine.
Condescending: prison inmate using rope to escape.
I’ve stated a business that checks Christmas cribs are up to standard. It’s called “QA in a Manger”.
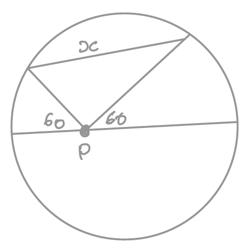
If the radius of the circle is 8 units, find x.
How can we solve this when we don't know where on the diameter point P lies? Well, the mere fact that we aren't told where but are still expected to solve the problem, supplies the extra information we need. The length x must be the same wherever P is.
Very well then, we can choose anywhere we like. So let's pick the centre of the circle.
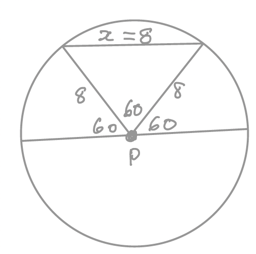
Now the angle marked in the triangle is 60 degrees, by subtraction from 180, and the two sides adjacent are radii of the circle, so their length is 8 units. Because of the 60 angle the triangle must be equilateral, and so the length of its third side is also 8.
So the answer is x = 8 units.
If there are five points on the surface of a sphere, then no matter how they are arranged at least four of them lie in the same hemisphere.
Proof: Pick any two of the points. These two points, taken with the centre of the sphere, define a plane that cuts the sphere into two hemispheres, both containing the points we picked.
Three points remain, and of these at least two must lie in the same hemisphere, which will then contain the required four points.
Can you prove that however the points are distributed it is always possible to draw a hemisphere that include at least four of the five points in its interior or on its boundary?
This puzzle appears in many places and was included in a maths competition as recently as the early 2000s. but I think it must go back further and may have first been published by Martin Gardner, although I don't have the reference.

Most native speakers of English will instinctively agree the order of the adjectives in my sentence above is wrong—weird even—without necessarily being able to describe exactly why; it flouts some rules that we all know but are not normally conscious of. These rules are difficult to write down precisely but roughly speaking follow a sort of semantic spectrum. The Cambridge Dictionary gives this order
opinion - size - physical nature - shape - age - colour - origin - material - type - purpose
If we rewrite my initial sentence using this order we get
which sounds perfectly normal, albeit a bit wordy perhaps.
Mu new dictionary—the one pictured—calls the rules "Adjectival order", although "Royal Order of Adjectives" is a more colourful name.
But "slaw" seemed a bit mysterious.
It turns out to be from Dutch, sla, slaw, a contraction of "salad", and we borrowed "coleslaw" directly from Dutch koolsla,"cabbage salad".
punctual: I’ll fight everyone
The answer is the expected proportion of Heads and Tails is 50:50.
A plausible intuition is that the strategy described in the problem with result in more Heads being observed than Tails, but this intuition is misleading
Each coin flip is independent and over a large number of trials Heads and Tails will each turn up with about the same frequency, and no strategy we might decide to follow can change this ratio.
I wrote a Python program to simulate the problem and sure enough if we run it Heads and Tails each appear in with about the same frequency.
import random
H = 0
for i in range(1000000):
throw = random.choice(['H','T'])
if throw != 'T':
H = H + 1
while throw != 'T':
throw = random.choice(['H','T'])
if throw != 'T':
H = H + 1
print('Heads per 1000000 Tails', H)
This blog might contain posts that are only visible to logged-in users, or where only logged-in users can comment. If you have an account on the system, please log in for full access.


