More dipping into really. It's Mathematical Puzzles: Revised Edition, by Peter Winkler. It's rather good, but I only stumbled across it by accident. Somehow (I can't remember how) I read a Guardian newspaper puzzle column and it contained this gem from Winler's book:
Find all the ways to arrange four points so that only two distances occur between any two of them.
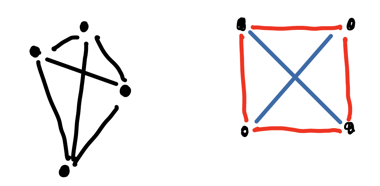
If you want to see the full solution the Guardian column provides a link to it.
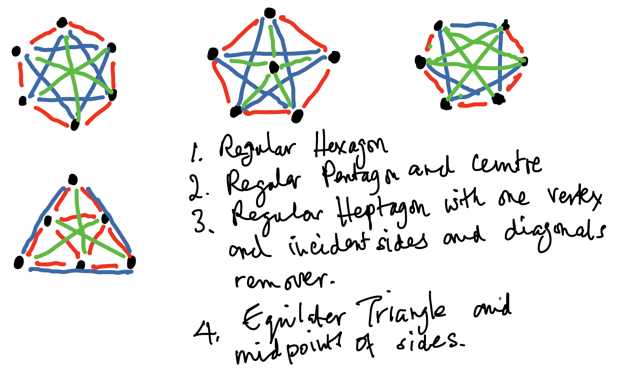
This got me thinking about related problems. With five points you can still keep to two distances but there is only one way (I think.) What about six points? Well, three different distances is the minimum possible number, but how many ways can it be done in? So far I have found four but I haven't tried yet to prove these are the only ones. Here are four I've found, with descriptions.