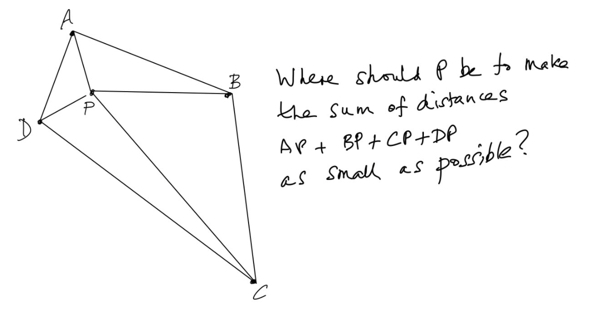
While I was having my dinner this puzzle occurred to me.
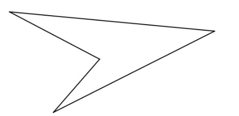
Assume the quadrilateral is convex, and has no re-entrant corners of the sort shown in this example.
After a bit of sketching quadrilaterals and points, I saw what the really beautiful answer is. Scroll down to read more.
.
.
.
.
.
.
.
.
.
.
.
.
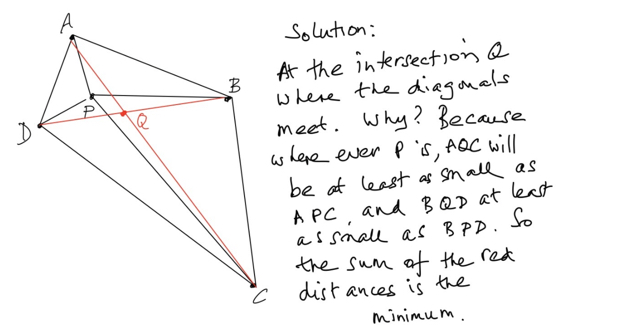
Then I went off to do some research, and of course there is nothing new under the sun. Fagnano wrote about this question ca. 1750. But similar questions still arouse research interest. Suppose we had different ways of measuring distance? Or we weren't on a flat surface? Or what about 4 points in space? Or more than 4 points in the plane?