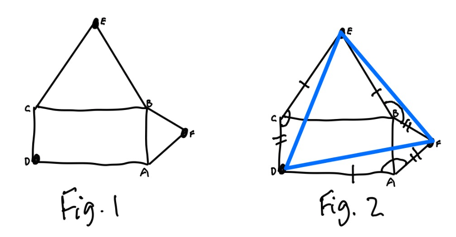
Suppose we take a rectangle and erect equilateral triangles on two of its side, as shown in Fig. 1. Show that pointsC, E and B are the vertices of an equilateral triangle.
Here is my proof: If we draw in the sides of the triangle (Fig. 2) we can see triangles DCE, BEF and DFA all have
a side of length | and one of length ||
an angle of 150 degrees included between those sides.
Consequently the three triangles are all congruent (the same as on another) and DE = EF = FD, so DEF is equilateral as required.