It seems counterintuitive that you can make a hole through a cube that will let a bigger cube pass through it. But you can.
The probem is named for Prince Rupert of Palantine (1619-1682), although he seems to have only asked about cubes of equal size. However it turns out that if the first cube has sides 1 unit long, a second cube of side just over 1.06 units can pass throught it.
The sketch below gives an indication of how this can be done.
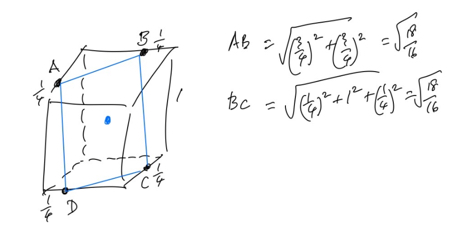
A, B, C and D are each 1/4 the way along an edge and using Pythagoras we find AB = BC = CD = DA which is just over 1.06. If we bore a hole perpenidicular to square ABCD with ABCD as cross-section then a cube of edge 1.06 can pass through the hole in the cube of edge 1.
Interestingly the distances AB, BC, CD, and DA are also equal if we measure them along the edges of the cube. 3/4 + 3/4 = 1/4 + 1 + 1/4.
Even more amazingly other solids such as a tetrahedron have the same property. For example it's possible to pass a tetrahedron through a hole in a smaller tetrahedron.