—You've probably seen this puzzle, which goes back to at least 1913 and was not new then.
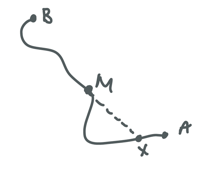
Three utility companies, Gas, Water and Electricity, want to each connect a supply to three houses, Nos. 1 and 2 and 3 Topology View. For technical reasons they do not want anyone's connect to cross another's. The sketch below shows a partial solution, in which 8 of the 9 connections required have been made without any crossings.
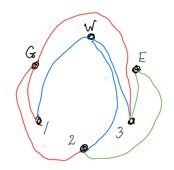
But making the last connection from E to No. 1 seems impossible without a crossing, and indeed it is. A particularly elegant proof is given in this Wikipedia article.
But all of this assumes we are working on a flat plane. What if we change the setting so that suppliers and houses are on a giant donut aka as a torus, as shown below?
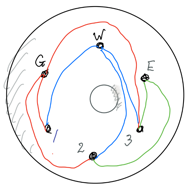
Well now we are on a torus we can take a path for E to No.1 that goes round the back of the torus, up through the hole in the middle, and connects to No.1, as indicated by the dotted line in the next sketch.
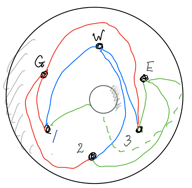
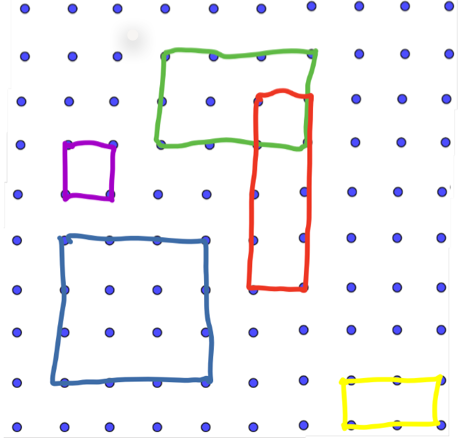
This configuration of two sets of three points (aka vertices), with lines (aka edges) between point in the first set and every point in the second is called the complete K3,3 which is reasonably self-explanatory. It is one of two "special" configurations, the other being K5 . K5 also cannot be drawn in the plane without a crossing, as we see in the next sketch.
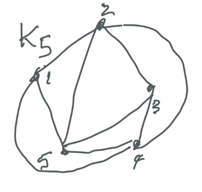
Although I have labelled it K5 that is not quite accurate, because it isn't complete; it ought to have 10 edges. However similar to K3,3 it is impossible to draw it in the plane without two edges crossing.
These two configurations are special because they let us answer the question "What, not necessarily complete, point and line configurations is it possible to draw in the plane without any crossing edges?" The answer is: exactly those configurations that contain no sub-configurations equivalent (in a fairly simple way but I'll skip the detail) to K3,3 or K5.
This is amazing, if you think about it: there are just these two forbidden sub-configurations and if they are avoided any point and line configuration whatsoever of the kinds we have been looking at can be drawn,"embedded", in the plane with no crossings.
Back to the torus. We have seen that K3,3 can be embedded in the surface of a torus, and so can K5 it turns out. In fact we can embed K4,4 (so we could fit in broadband too!) and K7. So we might ask: is there some set of forbidden configurations that let us say what can and cannot be embedded in the surface of a torus, similarly to the way we answered the question for the plane?
The answer is yes there is, but non-one can say yet how many forbidden sub-configurations there are. All that is known at present is that they number at least 17,523. That is the surprise alluded to in the title of this post. When I read that going from the plane to the torus involved a jump from 2 to 17,523 I was staggered!
And of course a torus has only one hole, but we could have 2, 3, 4,... holes and so on, so whatever happens there? It's mind-boggling!