I found this geometry problem posted a few days ago maths YouTuber Michael Penn. It was originally published in 2002 in the Mathematical Gazette. It caught my attention because Penn's solution and the one originally published seemed to use trigonometry and calculation of distances involving square roots, and I felt it should be possible to use a purely geometric approach.
After a lot of thought, by stepping outside the problem I think I've managed to solve it. Below left is the problem and at right the idea that set me on the right road. Suppose I drew in a square and an equilateral triangle to provide a context for the 45° and 30° angles, would that provide any insight?

This was nearly right, but then after more thought I saw a better approach was to use a square and an equilateral triangle of equal side length, like this.
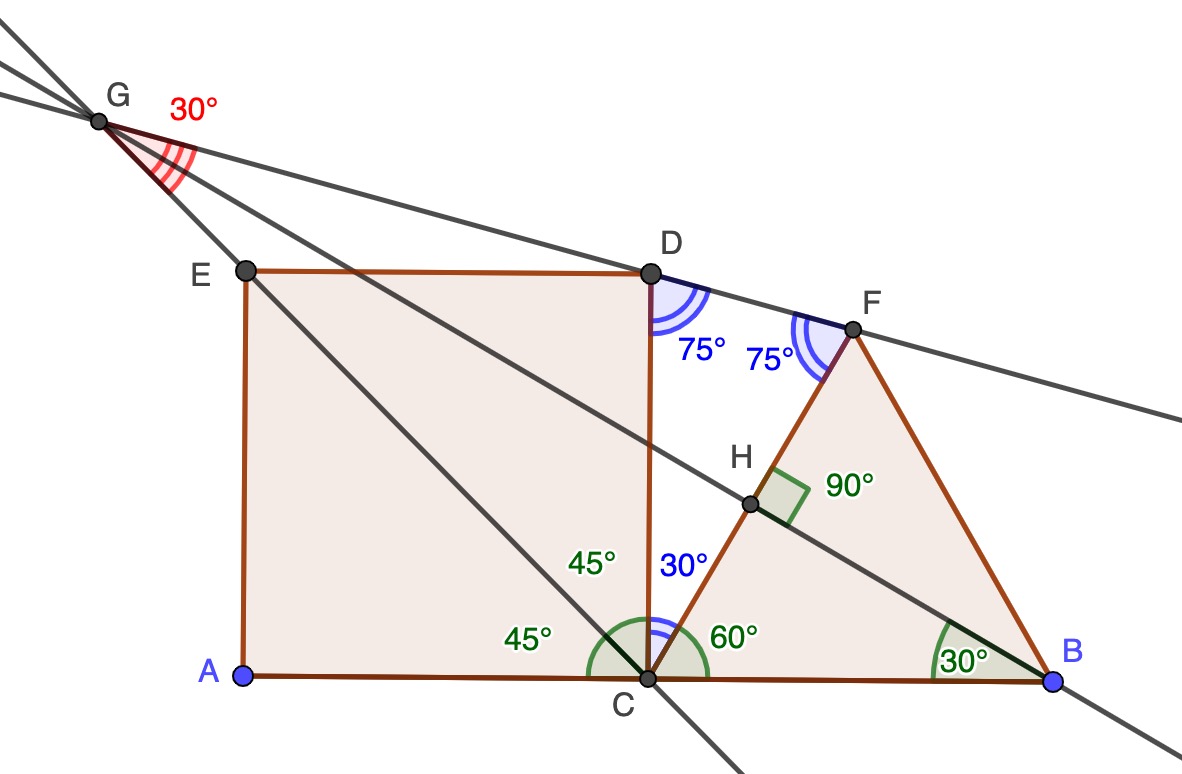
We can successively compute the angles marked in the diagram
is three stages.
1 (green angles marked by single arcs). At C we an internal
angle of the equilateral triangle, which is 60 degrees, and two angles which
are each half of a right angle, so they are 45 degrees. The line BG passes
through H, the midpoint of CF and from the symmetry of the equilateral triangle
we see that it makes a right angle with CF, and that the angle CBF is 30
degrees.
2 (blue angles marked by double arcs). The angles at C must
sum to 180 degrees, and so angle DCF must be 30 degrees.
CD = CF, because the square and the equilateral triangle
have equal side length, and so triangle CDF is isosceles. Hence the two angles
marked at D and C are equal and must both be 75 degrees because the angles of
CDF must add up to 180 degrees.
3 (red angle marked triple arcs). From consideration of the
angles in triangle CGF the angle marked at G must be 30 degrees.
Moreover, triangle CGE has two angles of 75 degrees and so it is isosceles.
Because the line through BH bisects the base of this triangle at right angles,
the triangle is symmetrical about the line, and the line must pass through
point G.
But where has the original problem gone you may ask? Dot in a line from G to A, and,Hey Presto! there it is in plain sight! The triangle shaded in with dots is the one in our problem.
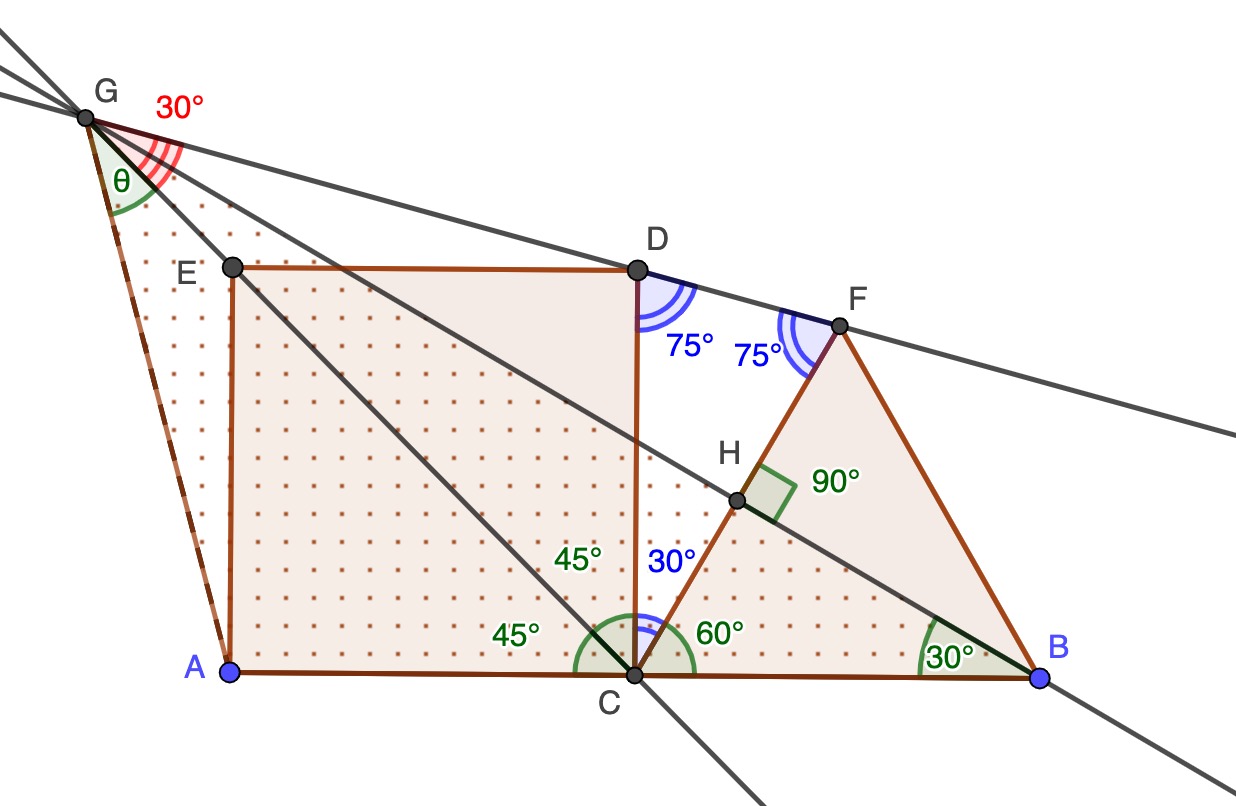
And now look at the kite AGDC. Can you see? - it is symmetrical about the diagonal CG, and therefore θ, the angle we are asked to find, is equal to angle CGD = 30 degrees. Problem solved.