In Algorithms 11 binding methods to an instance of a class getting dynamic dispatch was demonstrated: calling a method against an instance at a reference calls the method belonging to that object. Algorithms 12 showed class inheritance: inheritance of method names together with the functionality of those methods.
Together these two attributes provide subtype polymorphism: the ability to view an instance of a subclass as an instance of its super-class. Subtype polymorphism is enforced in statically typed languages where calling a method unknown to the nominal class of a reference (or by-value variable) gets a compile-time error. Python provides more or less total flexibility, a variable can be viewed as any type, but compliance with the framework supplied by static typing can provide a basis that is known to work.
The utility of class inheritance for building new classes from existing classes with added or specialised functionality is obvious: it saves work and reduces code size together with associated complexity. Copy and paste could be used to get a new type but using inheritance the total amount of code is reduced. In Algorithms 12 a Stack was turned into an extendable structure, a List, simply by replacing __init__() and push() with new methods and introducing a helper method _check_capacity().
Overriding and overloading methods
Replacing an inherited method is known as overriding the method. To maintain polymorphism the parameter types and return type of the new method must be the same as those of the overridden method or steps taken to ensure the new method still works when presented with the same type of arguments as the method being replaced. Stack.__init__() for example, was designed to accept an integer, the maximum size of a stack, so List's __init__() should also work when passed an integer as well as an Iterable. (Iterable is the base class of List and Python's list, so a new List can be constructed from either of these types).
A function's name, parameters and return type comprise its signature. Many statically typed languages allow use of functions with the same name but different signatures, known as overloaded functions or methods. From the compiler's viewpoint these are separate functions. This can cause problems in some languages when pre-compiled libraries are used because the overloaded function names exposed by the library have been changed by the compiler, a process known as name mangling.
Many languages allow functions to be called without their return being assigned to a variable. In this case the expected return type will be unknown to the compiler so the signature used for overloading excludes the return type. When overloading is available execution efficiency will suffer if the type of a parameter is chosen to be that of a mutual ancestor with runtime type checking used to determine the actual type rather than writing separate overloaded methods for the different types.
Pythons dispatch mechanism uses the method name to determine which method to call. Parameter types do not feature in this selection excluding overloading. Any method with the same name in a subclass effectively overrides the superclass method but complete flexibility as to the type of parameters passed to a function can replace overloading. Runtime type checking or named default parameters are used to determine how parameters of different types are processed. Named defaults are considered to be more 'Pythonic' but are less transparent in use.
Encapsulation
Coding abstract data types without OOP in languages such as UCSD Pascal, Ada83 and Delphi there can be complete separation of operations appearing in the interface from the workings hidden in the implementation. Anything declared in the implementation, perhaps located in a separate file is private and hidden in entirety from client code.
Interface / implementation separation has become known as information hiding, a term originating from the design strategy proposed by David Parnas (Parnas 1972). In OOP such separation is provided by encapsulation but the facilities available to achieve it vary from one language to another. In general encapsulation means grouping the methods that operate on data with the data rather than passing data objects with no inherent functionality to a hierarchy of possibly shared subroutines.
OOP languages tend to declare all fields and methods in an interface file or section hiding only method implementations or feature no physical separation of code the entire class appearing in a single file. A typical C++ program for example will define a class in a .hpp header file and put method implementations in a separate .cpp file.
In C++ any class that is not defined as abstract can be instantiated by value simply by declaring a variable of the class. In this case the compiler needs access to the total size of fields so sufficient space can be allocated to accommodate the instance. When all instances are by reference as in Java etc. this is not a requirement. All references have the same size in memory and the actual allocation is done at runtime by object creation. Even so, Java and many other languages still feature all-in-one-place class definitions.
To overcome implementation exposure two strategies have been adopted: inheritance from a pure abstract class or interface type without any fields featuring only method definitions and secondly, key words defining levels of exposure for the members of a class (its methods and fields), generally private, protected and public.
With inheritance from an abstract class descendant instances can be assigned to a reference of the abstract type and viewed as such. The descendant supports the interface defined by the superclass. Languages that do not provide multiple inheritance generally define an interface type and a class can support multiple interfaces. The actual implementation can be ignored by client code and can be made reasonably inaccessible through the reference providing interface / implementation separation. This comes at the cost of pre-definition of the abstract type and perhaps an additional execution overhead resulting from multiple inheritance.
Beyond the separation of the interface as a set of public methods, other levels of exposure only relate to re-use of functionality through inheritance. Fields and methods defined as private are hidden from client code and in subclasses. Those defined as protected are inaccessible to client code but are visible in a subclass implementation.
Making fields and methods private imposes restrictions on the options available when writing a subclass. For example, a base class Person might have a private field date_of_birth. If modification to this birthdate after instantiation is a requirement a public method set_birthdate() is needed. A subclass, Employee say, must either use the inherited setter method or override it perhaps to ensure that no person below a certain age can be employed. An overridden setter cannot access the private field but calls the inherited setter to modify the birth date. This minimum age requirement is then imposed on all subclasses of Employee, not so if date_of_birth had been give protected exposure.
Sounds logical but such a lack of flexibility can cause problems when the only access a descendant of employee can have to the age field is through the inherited setter. Suppose at a later time a new class Trainee is required with a lower age limit. Due to the imposed limit no Trainee can be an Employee and cannot inherit or take advantage of any functionality already written in relation to employees. Reducing the limit for Employee will likely break existing age verification.
Another consideration may be the additional overhead of methods that call other methods, not good when execution efficiency is in any way critical. To overcome these problems Java provides a fourth level of exposure known as 'package-private', the default when no other is specified. All Java classes exist in a package, a grouping of class files. Package-private members of are visible in the implementation of all other classes in the same package but inaccessible to classes located in other packages.
Package-private exposure finds widespread use in supplied Java class libraries and many other languages provide an equivalent. Using it as an alternative to protected exposure is all very well if it is possible to extend a package, not a possibility for these Java libraries. Consequently minor modifications to the functionality of a HashMap say, with a requirement for equivalent execution efficiency means starting almost from scratch. The only useful library definition is the Map interface.
Coding descendants there is really very little to be gained from these restrictions and making the implementation completely inaccessible is not possible in Python. Protected and private categorization is available by a naming convention rather than error generation and more reliance is placed on organization and coding by thinking. Similar measures are available for structuring the code to provide modularity.
Python information hiding
The smallest increment of Python functionality is a class. Classes can contain nested classes but putting a class in a nested location has no particular significance other than an indication of associated usage. For an inner instance to have knowledge of an enclosing object it must be given a reference to it:
class Outer(object):
class Nested:
def __init__(self, outer):
self._outer = outer
...
def __init__(self):
self._inner = Outer.Nested(self)
...
Python provides no direct equivalent of private and protected exposure but a convention that variable and helper method names starting with an underscore are protected and should not be accessed directly by client code is useful. A leading double underscore supplies some equivalence to private members but this provision is not required in most cases.
Constants exposed by a module can be put in all upper case to indicate their status but to get a constant that is immutable as far as possible it must be made a member of a class accessible through a property. This option is shown in the download package1.module2 but going to these lengths is not what Python is about, I think.
Python, Delphi, C# and some dialects of C++, provide so called properties, a construct that replaces public getter and setter methods generally to control or exclude modification of the value of private or protected fields by client code. The property is seen as a virtual field so we can write x = aproperty and when write modification has been programmed aproperty = x, both without function-call brackets or arguments.
Because all members are accessed by name in Python its properties can supply validation of submitted values in a subclass even if the base class provides direct access. A property with the name of the base class field replaces it. A number of different syntax and variations are available but typical usage might be:
class Base:
def __init__(self, value):
self.value = value # value is a fully accessible field
def halve(self):
self.value /= 2class Subclass(Base):
def _get_value(self):
return self.value
def _set_value(self, value):
if value >= 0 and value < 100:
self.value = value
val = property(_get_value, _set_value)
instance = Subclass(99)
print(instance.val)
instance.halve()
print(instance.val)
In the Subclass the property value replaces the base class field and all inherited methods now address the field _value through the setter and getter functions. The base class field value does not exist in the subclass so there is no wasted allocation.
In Subclass the field name _value could have been given a double underscore indicating private status. Doing this invokes name-mangling and __value becomes an alias for the mangled name in the implementation. The mangled name, which always follows the pattern _Base__value or generically _Classname__membername, is visible in subclasses and client code as well as the current implementation. Such members are not truly private, simply less accessible to erroneous use.
Double underscore method names can be used to get the same effect as the static instance methods available in C++ etc. When a dynamically dispatched method is overridden this directs all calls to the new method, very likely an unwanted side effect when the method is a helper used by multiple other inherited methods. Replacing a static method in a subclass, same name, same signature, this does not occur and any calls in inherited methods still go to the superclass method.
The two alternatives are contrasted by mod_list.py and mod_list_static.py in the download. An overridden _check_capacity() method and a 'static' equivalent __check_capacity()are shown as respective alternatives. The replaced method is used in a subclass by insert_at() but not push(), which must continue to use the inherited version.
Python modules and packages
A Python file or 'module' with a .py extension can contain constants, variables, functions and class definitions. In larger programs modules supply the next increment of modularity above classes. Lest we forget which module is being used, within a module its canonical name is available through the global variable __name__. However, when a module is run as a program __name__ is set to '__main__' getting the option of excluding minor test code from module initialization by enclosing it in an if statement. Variability of __name__ is demonstrated in package1.module1 together with the options for importing modules contained in a package as shown below.
The same naming conventions using underscores to indicate modules that are only for use by modules in the same package can be employed but a prepended double underscore does not result in name-mangling.
Packages allow modules to be grouped according to the type of functionality they expose or the usage they have within an application. They can be nested to any depth: package1.sub_package.subsub_package.subsub_module. When importing a module no account is taken of the location of the importing module in the package hierarchy and the full canonical path must be used.
If package1 contains two modules module1 and module2, to import a function module2.where() to module1 there are three options:
import package1.module2 # import option 1
from package1 import module2 # import option 2 (recommended)
from package1.module2 import where as where2 # import option 3
def where():
return __name__
def elsewhere():
result = package1.module2.where() # using import option 1
result = module2.where() # using import option 2
result = where2() # using import option 3
return result
if __name__ == '__main__':
print(where())
print(elsewhere())
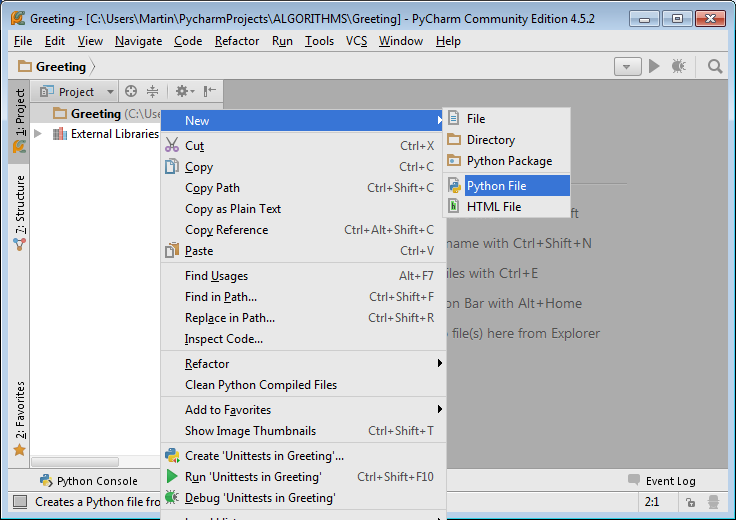
To create a new package in PyCharm, in the project tree right-click on the project name or the package under which the new package is to be created and select new > Python Package. PyCharm creates a module __init__ within the new package. The purpose of this module is to code any package initialization not done by constituent modules. When __init__ does not declare an __all__ list of module names, any modules imported to it from the current package or elsewhere are made visible in any module using the statement:
from package import *
When the alternative, declaring a list of modules in __init__ to be imported by import * is used, __all__ = ['module1', 'module2'] for example, this list can contain only modules in the immediate package. Also its presence excludes access to the modules in __init__'s import statements as described above.
Note that circular imports are not allowed. If module1 imports module2 then module2 cannot import module1. It may be possible to circumvent this rule by importing individual items, as in import option 3 above and module2's equivalent of module1's elsewhere() in the download, but be aware of possible problems: type checking failing to recognize an imported class for example.
Summary
Interface / implementation separation isolates client code from changes to an implementation. It can also provide levels of abstraction, used to mitigate the complexity inherent to large software systems. A user interface for example, can hide its implementation and the various subsystems that support it. Similarly each subsystem can hide its own implementation from code in the user interface. This layering of functionality can continue down through as many levels as may be required following the design strategy of information hiding.
OOP languages provide a level of interface, implementation separation through encapsulation. Subtype polymorphism used with abstract or interface classes can strengthen encapsulation. If sufficient pre-planning is put in place, provision of read-only interfaces for example, object integrity can be ensured.
Python relies less on enforced encapsulation than on code written with the precepts of information hiding in mind. Python's call-by-name has two effects here: any class supplies a conceptual interface that can be supported by any other class supplying the same function names and exposed functionality; direct access to fields in a base class can be overridden using properties.
Import statements within the __init__ module can be used to create virtual groupings exposing modules and/or classes from other packages. This facility suggests the option of creating multiple groupings by type of functionality and by usage within an application, for example.
Reference
Parnas, D. L. (1972) 'On the Criteria To Be Used in Decomposing Systems into Modules', Communications of the ACM, vol 15 no. 12 [Online]. Available at https://www.cs.umd.edu/class/spring2003/cmsc838p/Design/criteria.pdf (Accessed 22 September 2015)
[Algorithms 14: Subtype polymorphism and encapsulation (c) Martin Humby 2015]