See:
https://learn1.open.ac.uk/mod/oublog/viewpost.php?post=260010
I found this in a puzzle book and thought it would be not too hard, but it was more tricky than I expected. Making sure you haven't missed any triangles, or double counted any, is quite slippery.
Here are the possible kinds of triangle:
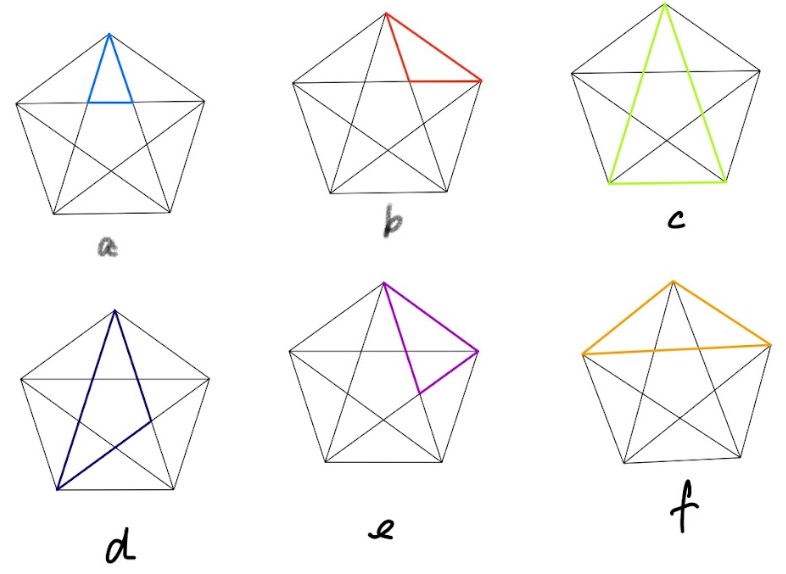
Each of these can occur in five positions, so I thought at first the answer is 6 x 5 = 30, but I was mistaken, because config. e has chirality, i.e. handedness; the triangles can be aligned right or left, and so we get a total of 35.
After more investigation I found a fairly recent paper which gives a general formula for a regular polygon with any numbers of sides, but for larger numbers it gets quite complicated.
I liked this problem, for the original pentagonal case, because it is easy to grasp, less simple than appears at first but is still solvable with some careful working.
I'll post a link to the paper about the general case for anyone interested.