I went to the Doctor, I said "Every night while I'm asleep I keep imagining I'm the fraction ⅓ expressed as a decimal." The Doctor said "Nothing to worry about. Lots of people have recurring dreams."
Personal Blogs
While reading the WikiQuote entry for Niels Bohr I came across a striking picture of the stained glass windows in the spire of the Thanksgiving chapel in Dallas.
Recently some of my decimals ran away. But I managed to round them all up.

This famous painting by Caspar David Friederic is entitled Wanderer above the Sea of Fog. To me it's a kind of commentary on the human condition, but also a perspective on what may have inspired Newton, Einstein, and so many others.
pruritic
= causing itching. From Latin prūrīre, to itch.
pigritude
= laziness or sloth
Surprisingly, the name of this bird seems to come, ultimately, via Anglo-Norman and Latin, from Ancient Greek πέρδεσθαι, perthesthai, to break wind. It’s believed to be imitative of the rapid whirring of a partridge’s wings as it takes off from the ground (if you have ever heard this sound you’ll recognise the resemblance). The word fart comes from the same root.
I found this quote today
“The important thing is not to stop questioning. Curiosity has its own reason for existence. One cannot help but be in awe when he contemplates the mysteries of eternity, of life, of the marvelous structure of reality. It is enough if one tries merely to comprehend a little of this mystery each day.”

When icicles hang by the wall,
And Dick the shepherd blows his nail,
And Tom bears logs into the hall,
And milk comes frozen home in pail.
William Shakespeare
Photo by my brother Simon
It seems counterintuitive that you can make a hole through a cube that will let a bigger cube pass through it. But you can.
The probem is named for Prince Rupert of Palantine (1619-1682), although he seems to have only asked about cubes of equal size. However it turns out that if the first cube has sides 1 unit long, a second cube of side just over 1.06 units can pass throught it.
The sketch below gives an indication of how this can be done.
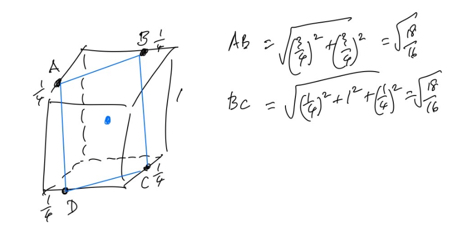
A, B, C and D are each 1/4 the way along an edge and using Pythagoras we find AB = BC = CD = DA which is just over 1.06. If we bore a hole perpenidicular to square ABCD with ABCD as cross-section then a cube of edge 1.06 can pass through the hole in the cube of edge 1.
Interestingly the distances AB, BC, CD, and DA are also equal if we measure them along the edges of the cube. 3/4 + 3/4 = 1/4 + 1 + 1/4.
Even more amazingly other solids such as a tetrahedron have the same property. For example it's possible to pass a tetrahedron through a hole in a smaller tetrahedron.
In Philosophy you’ve got to tread carefully. It’s a mind field.
Q. What would you call rice arranged in a column?
A. Pillar rice.
“This leg-wear once belonged to a very eminent person”, said Tom grandiosely.
I find ironing clothes so tedious nowadays. I guess I’m just ironing bored.
Flowers in my garden

Sad news. The inventor of the Roulette wheel has cashed in his chips.
“I forbid you to go to the dance contest”, said Tom strictly.
It seems the underworld have an award for the most successful attempt to influence a jury. It’s known as the nobble prize.
I’ve been asked for a joke about German cheese. I’m on the Käse.
E was just an ordinary vowel really. Much like U and I.
What do you call it when a sheep is stopped for speeding?
A woolly pullover.
My vacuum cleaner should suck.
It doesn’t suck.
Therefore, it sucks.
Not many people know this but the US has a heavily-guarded facility where enormous quantities of string are stored. It’s called Fort Knots.
This blog might contain posts that are only visible to logged-in users, or where only logged-in users can comment. If you have an account on the system, please log in for full access.

