My crystal ball broke down so I took it back to the shop. They said they’d look into it.
Personal Blogs
A friend travelling in the Eastern Caribbean sent me some photos of flowers. This lovely plant is paperflower, or lesser bougainvillea, scientific name Bougainvillea glabra.

I'm disbelieving of this being a Harvard Interview Question, but that is the title given to a question circulating on social media. It runs as follows:
| "7 men have 7 wives. Each man and each wife have 7 children. What's the total number of people?" |
|---|
It's ambiguous and that's probably why it has gone viral, with people offering a variety of answers and opinions and even the occasional quip, such as "Were they going to St Ives?".
So it's not the maths that is interesting but the impetus to debate, discuss wrangle, argue. disagree and tut about the ambiguity.
Still, to get back to the boring old maths, I thought I would ask:
If 7 is replaced by n, what is the smallest answer that we could put forward a case for, and what is the largest?
If Musk got involved in a cover-up, would it be stretching things to call it Elongate?

Annie L. Pressland (1862-1933), from Wikimedia
A GPS is one that "leads you down the garden path". As you read it you think you are understanding it, then it socks you on the back of the head ("This makes no sense") but finally you realise you'd been reading it the wrong way and it makes sense after all. The canonical example is
"The old man the boat."
Another one, that is really hard to parse, is
"The complex houses married and single soldiers and their families."
Eh?#%~
The Wikipedia article says the first example "has been used to test the capabilities of artificial intelligence efforts" but that was in 2016, and today DeepSeek has no trouble, it's seen it before and can analyse it with no difficulty at all
I thought I would try making up my own GPS
Here's my attempt at a GPS sentence. It took me several goes before I was able to work the idea up into something that met DeepSeek's quite stringent criteria for a bona fide example but I finally came up with this which earned its seal of approval.
"The hack saw the editor."
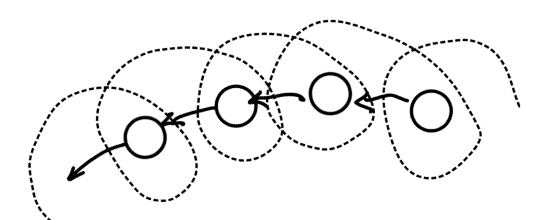
We know that from a Sun-centred point of view the Earth goes around the Sun and the Moon round the Earth. If we could magically hover above the plane of the Sun-Earth-Moon system, remaining at rest relative to the Sun, what would the path of the Moon look like from that vantage point?
Intuitively I thought it would trace a loopy path, something like the dotted trajectory in my sketch below.
I was surprised to find out how wrong my intuition was. The actual path is like the one below, which was generated by an nice simulation from the University of Colorado [1].
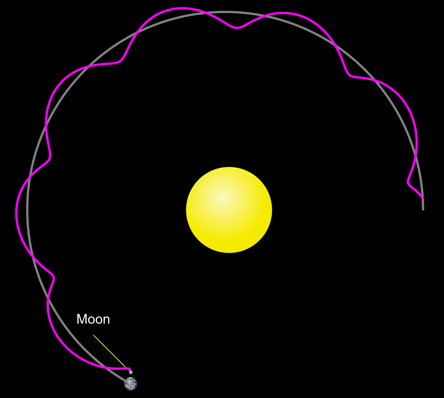
This is not to scale of course, the diameter of the Earth is about 8,000 mi and the distance from the Earth to the Sun 93,000,000 mi so if the orbit were drawn to scale your screen would need to be (roughly) 40 m wide, or the Earth drawn so small it would be a speck.
[1] https://phet.colorado.edu/sims/html/gravity-and-orbits/latest/gravity-and-orbits_all.html
The sentence below (perhaps seen on a sign in a hospital) was discussed in a 1979 paper by Watson and Reich [1] and has attracted a good deal of interest in the intervening years.

What does it mean? Whoever wrote it presumably meant "Don't ignore a head injury however trivial it is", and that is what most people read it as, but if we unpick the wording carefully that is not what it literally means.
Compare it with "No citizen is too poor to be taxed" which says that no citizen is so poor as to be exempt from being taxed, i.e. all citizens are taxed. So it seems the hospital sign has a meaning opposite to the intended one.
A friend said she thought I must have some phobia about tidiness (what, me?) so I wondered if there is a word for such a condition. There wasn't but there is now, because I invented it.
Eutaxiophobia
Etymology : from Ancient Greek eu- (εὖ) "good" + taxis (τάξις) "arrangement" + phobia (φόβος) "fear"
Then I validated my new word by asking DeepSeek what it meant. It told me that it was not a commonly recognised word but if it existed it would mean "a fear or aversion to orderliness or tidiness", which fits the bill perfectly.
It's possible I am not the only person with this particular phobia.
Easy really, it’s just comma sense.
oscine : pertaining to songbirds
This word came into English from Modern Latin in the late 19th century. The ancient Latin word is oscen, whose elements according to Etymonline are ob- and canere "to sing". These in turn have Proto-Indo-European origins, epi-, which has a broad prepositional meaning of spatial nearness and kan-, "to sing".
Other words that seem to be from kan_ include accent, charm, descant, enchantment and Carmen, and many others.
Oscine is a rare word. I came across it in Times 2 Word watch column and I'd never seen it before. It only occurs on average 0.01 times per million words. So in this blog post it has come up with a frequency that would normally only appear once in every 200 million words.
If two chords of a circle intersect there is a neat relationship between the lengths of the four line segments created, as seen below.
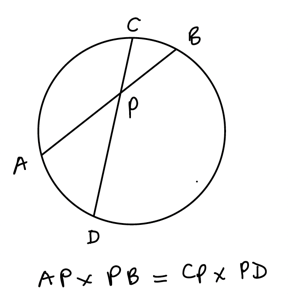
This neat theorem must go back to the ancient Greek geometers. It's a fairly simple relationship but quite powerful and it often provides a short and elegant solution to geometric problems I used it yesterday to solve Think You Can Solve This? Find the Square’s Area!, posted on YouTube by "The Phantom of the Math".
The Phantom's question boils down to finding the side length of the square in the configuration below, where the square is divided by horizontal and vertical lines of symmetry as shown, the circle has its centre on the vertical symmetry line, and the circle is 3 units and 4 units away from the left-hand and top sides of the square.
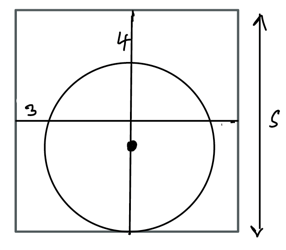
The standard approach to this sort of problem is to construct a right-angles triangle, come up with expressions for the lengths of its side, then use Pythagoras to arrive at an equation which we can then go on to solve. I used this approach, then when I had an answer I went back to see how the Phantom had tackled it, and as I. expected they had followed a similar strategy.
But the problem nagged at me, because these solutions were a bit involved and mechanical and I felt there ought to be a better way. After pondering on and off for quite a while I suddenly saw a pair of intersecting chords right in front of me! Now the solution fell out really easily, like this
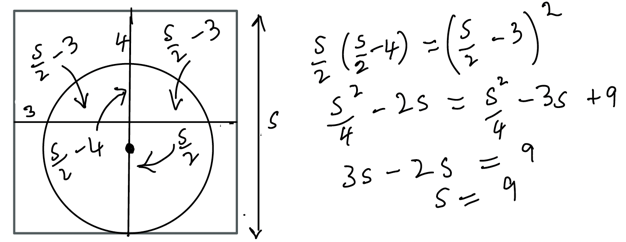
Finding the lengths of the four segments in terms of the side length s is not hard, we apply the intersecting chords theorem, expand and tidy up, then it's easy to solve the equation and find that s = 9 units. No applications of Pythagoras were used in this solution, and no extra lines needed to be added!
The person who invented momentum (was it Isaac Newton?) was originally going to call it 'moment' but at the very last moment they hesitated.
If you had to pick a size of spiritualist, what would you go for?

The Art of Uncertainty, by David Spiegelhalter, someone who I have long admired. I watched an Oxford Mathematics Public Lecture Chance, luck, and ignorance on YouTube and really liked the content and the way he presented it.
Early in the talk he quotes an Italian statistician de Finetti who famously declared "probability does not exist". Spiegelhalter goes on the say that after 50 years of mulling things over he has decided that Finetti was right! I don't think he is claiming that we can't attach numbers to whether we think some event will happen or not, only that probability (with the possible exception of subatomic particles) probability is not a property of the world but something humans have made up, a "personal expression of our uncertainty".
By this point he had won me over and I bought the book. The lecture, which I watched right through was fascinating. Towards the end he gave an arresting example using a pack of playing cards as a prop.
Randomly shuffle a pack of cards*. Now the order of cards has almost certainly never, ever happened before in the entire history of humankind. If every person ever born had lived to be 100 and shuffled a pack of cards every second of those 100 years the chance of any of them having generated the same order as the pack you hold in your hands is infinitesimally small. Here are the sums:
Estimated number human who have ever lived 120 billion
Seconds in 100 years about 3 billion
So all those people shuffling away could have produced only(!) 120,000,000,000 x 3,000,000,000
= 360,000,000,000,000,000,000 = 3.6 x 1020 shuffles. Let's call it 4 x 1020 to simplify the arithmetic coming in a moment.
But the total number of ways to order the pack is 52 x 51 x 50 x ... x 3 x 2 x 1 = 52 factorial, which my calculator says is about 8 x 1067.
That means the chance that one of those people generated the same order as you is
4 x 1020 ÷ 8 x 1067 which is 1 in 4 with 47 zeros after it
It's theoretically possible but the chances it will are almost unimaginable small.
* To do this properly you need to do at least 7 successive riffle shuffles or 1 minute of "smooshing", see the fascinating Numberphile video The Best (and Worst) Ways to Shuffle Cards. Anything less than this the pack is probably not truly randomised.

this winter nightfall
the trees stretch their branches up
reaching for the moon
I came across this crossword clue
It goes round and round again (5)*
So I downloaded a list of 370,105 words from dwyl/english-words on GitHub, and wrote a short Python program to extract all the words that are the same backwards as forwards. My program found 232 reversible words, which appear in the list below. Some of them are rare or debatable – I certainly don't know what most of them mean – but there are plenty of familiar words there.
The longest is 'kinnikinnik', which is in the OED and means
A substance used by some Indigenous peoples of North America as a substitute for tobacco or for mixing with it, typically consisting of dried sumac leaves and the inner bark of willow or dogwood.
a, aa, aaa, aba, abba, acca, ada, adda, addda, adinida, affa, aga, aha, ajaja, aka, akka, ala, alala, alula, ama, amma, ana, anana, anna, apa, ara, arara, asa, ata, atta, ava, awa, b, bab, bb, bib, bob, boob, bub, c, cc, cyc, civic, crc, csc, d, dad, dd, deed, deedeed, degged, deified, deked, deled, denned, dewed, did, divid, dod, dtd, dud, e, ecce, ee, eye, eke, elle, eme, ere, ese, esse, eve, ewe, f, ff, g, gag, gig, gog, goog, h, hagigah, hah, halalah, hallah, heh, huh, i, y, yay, yaray, ihi, ii, iii, imi, immi, yoy, j, k, kaiak, kayak, kakkak, kassak, kazak, keek, kelek, kinnikinnik, kook, l, lemel, level, ll, lwl, m, maam, madam, malayalam, malam, mallam, mam, marram, mem, mesem, mim, mym, minim, mm, mmmm, mom, mum, murdrum, n, nan, neven, non, noon, nun, o, ofo, oho, ono, oooo, oto, ottetto, otto, p, pap, peep, peeweep, pep, pip, poop, pop, pp, prp, ptp, pup, q, r, radar, redder, refer, reifier, renner, repaper, retter, rever, reviver, rotator, rotor, s, sagas, samas, sds, sees, selles, sememes, semes, senones, seres, sexes, shahs, siris, sis, solos, sooloos, sos, sps, ss, stats, stets, succus, sus, t, tat, tebbet, tebet, teet, tenet, terret, tgt, tibbit, tipit, tirrit, tit, tyt, tkt, tnt, toot, tot, trt, tst, tut, txt, u, ulu, ululu, umu, uru, usu, utu, v, vav, vv, w, waw, wow, x, xix, xx, xxx, z.
* rotor
The shopkeep said, "I can let you have three. Then that's your lot."

Hail is from OE hagol, which may ultimately be related to Latin calix and Greek κάχληξ, pebble, and so from the same origin as calcium.
enclose : indeterminate number of clothes
It being Burn's Night I had haggis with the neeps and tatties and for afters this cranachan, which was very nice indeed.

The OED defines the name like this
Scottish.
"A dessert typically made with whipped cream, whisky, oatmeal, honey, and berries (esp. raspberries)."
and although it must be traditional the first citation the OED gives is from 1946.
Previously I posted a well known problem which asks: suppose we are on a circular boating lake when fog descends. We know the size and shape of the lake and can travel any distance and in any direction we please, but we don't know where we are on the lake, so we are rowing blind. What is the shortest distance we must be prepared to row to be sure of escaping from the pond. and what path should we follow?
The answer is that you should row in the straight line until you hit the bank and may have to travel a distance equal to the diameter of the pond, and this cannot be improved on. My proof is here. I actually found this for myself some years ago but it turned out to have already been published 40 year before. so I was late to the party.
A follow up question was: what if we are on a pond in the shape of an equilateral triangle? The diameter of an equilateral triangle is just the length of one of its sides and this is the least escape distance if you keep to a straight line. But rather surprisingly (well I think it is) a zig-zag escape path exists which is shorter, at about 0.98198 of the side length.
Here are two pictures of the path in different positions and you can probably see how it manages to always reach the perimeter of the triangle even though it is shorter than the diameter.

This blog might contain posts that are only visible to logged-in users, or where only logged-in users can comment. If you have an account on the system, please log in for full access.